Lernziele
Ein experimentelles Phänomen, das mit der klassischen Physik nicht ausreichend erklärt werden kann, ist die Schwarzkörperstrahlung. Lernziele für diesen Abschnitt sind
- Mit Schwarzkörperstrahlern vertraut sein
- Das Stefan-Boltmann-Gesetz anwenden, um die Gesamtlichtleistung eines Strahlers abzuschätzen
- Das Wiensche Verschiebungsgesetz anwenden, um die Spitzenwellenlänge (oder Frequenz) der Leistung eines Schwarzkörperstrahlers abzuschätzen
- Das Rayleigh-Jeans-Gesetz und wie es die Strahlung Schwarzer Körper nicht richtig modelliert
Alle normale Materie bei Temperaturen über dem absoluten Nullpunkt sendet elektromagnetische Strahlung aus, Diese stellt eine Umwandlung der inneren Wärmeenergie eines Körpers in elektromagnetische Energie dar und wird daher als Wärmestrahlung bezeichnet. Umgekehrt absorbiert alle normale Materie elektromagnetische Strahlung bis zu einem gewissen Grad. Ein Objekt, das ALLE Strahlung, die auf es fällt, bei allen Wellenlängen absorbiert, wird als Schwarzer Körper bezeichnet. Wenn ein Schwarzer Körper eine gleichmäßige Temperatur hat, hat seine Emission eine charakteristische Frequenzverteilung, die von der Temperatur abhängt. Diese Emission wird als Schwarzkörperstrahlung bezeichnet.
Ein Schwarzkörper bei Raumtemperatur erscheint schwarz, da der größte Teil der von ihm abgestrahlten Energie im Infrarotbereich liegt und vom menschlichen Auge nicht wahrgenommen werden kann. Da das menschliche Auge Lichtwellen bei niedrigeren Frequenzen nicht wahrnehmen kann, erscheint ein schwarzer Körper bei der niedrigsten gerade noch sichtbaren Temperatur im Dunkeln betrachtet subjektiv grau, obwohl sein objektives physikalisches Spektrum im Infrarotbereich gipfelt. Wenn er etwas heißer wird, erscheint er mattrot. Mit weiter steigender Temperatur wird es gelb, weiß und schließlich blau-weiß.

Schwarzkörperstrahlung hat ein charakteristisches, kontinuierliches Frequenzspektrum, das experimentell nur von der Temperatur des Körpers abhängt. Tatsächlich können wir viel genauer sein:
Ein Körper emittiert Strahlung bei einer bestimmten Temperatur und Frequenz genau so gut, wie er dieselbe Strahlung absorbiert.
Diese Aussage wurde von Gustav Kirchhoff bewiesen: Der wesentliche Punkt ist, dass, wenn wir stattdessen annehmen, dass ein bestimmter Körper besser absorbieren kann, als er emittiert, dann wird er in einem Raum voller Objekte, die alle die gleiche Temperatur haben, die Strahlung von den anderen Körpern besser absorbieren, als er Energie an sie zurückstrahlt. Das heißt, er wird heißer und der Rest des Raumes wird kälter, was dem zweiten Hauptsatz der Thermodynamik widerspricht. Um den zweiten Hauptsatz der Thermodynamik nicht zu verletzen, muss ein Körper bei einer gegebenen Temperatur und Frequenz genau so viel Strahlung aussenden, wie er absorbiert.
Jeder Körper strahlt bei einer Temperatur oberhalb des absoluten Nullpunkts in gewissem Maße, wobei die Intensität und Frequenzverteilung der Strahlung von der detaillierten Struktur des Körpers abhängt. Um mit der Analyse der Wärmestrahlung zu beginnen, müssen wir den Körper, der die Strahlung abgibt, genau beschreiben: der einfachste mögliche Fall ist ein idealisierter Körper, der ein perfekter Absorber und daher auch (aus dem obigen Argument) ein perfekter Emitter ist. Wie konstruiert man also einen perfekten Absorber im Labor? Kirchhoff hatte 1859 eine gute Idee: Ein kleines Loch in der Seite eines großen Kastens ist ein hervorragender Absorber, da jede Strahlung, die durch das Loch hindurchgeht, im Inneren abprallt, wobei bei jedem Aufprall viel absorbiert wird, und kaum eine Chance hat, jemals wieder herauszukommen. Wir können das also umgekehrt machen: Wir haben einen Ofen mit einem winzigen Loch in der Seite, und vermutlich ist die Strahlung, die aus dem Loch kommt, so gut wie ein perfekter Strahler, den wir finden werden (Abbildung \(\PageIndex{2}\)).
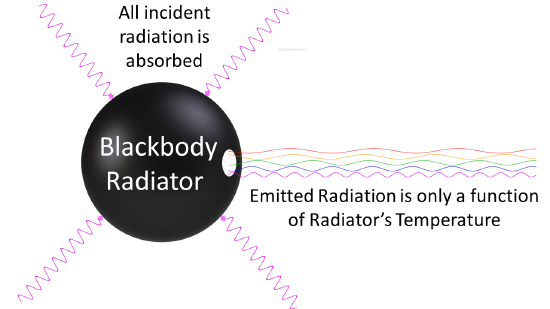
In den 1890er Jahren hatten sich die experimentellen Techniken soweit verbessert, dass es möglich war, ziemlich genaue Messungen der Energieverteilung von Schwarzkörper-Strahlung durchzuführen. Im Jahr 1895 stanzten Wien und Lummer an der Universität Berlin ein kleines Loch in die Seite eines ansonsten vollständig geschlossenen Ofens und begannen, die austretende Strahlung zu messen. Der aus dem Loch austretende Strahl wurde durch ein Beugungsgitter geleitet, das die verschiedenen Wellenlängen/Frequenzen in unterschiedliche Richtungen schickte, alle in Richtung eines Bildschirms. Ein Detektor wurde entlang des Schirms auf und ab bewegt, um herauszufinden, wie viel Strahlungsenergie in jedem Frequenzbereich emittiert wurde. Sie fanden eine Strahlungsintensität/Frequenzkurve, die den Verteilungen in Abbildung \(\PageIndex{3}\) nahe kommt.
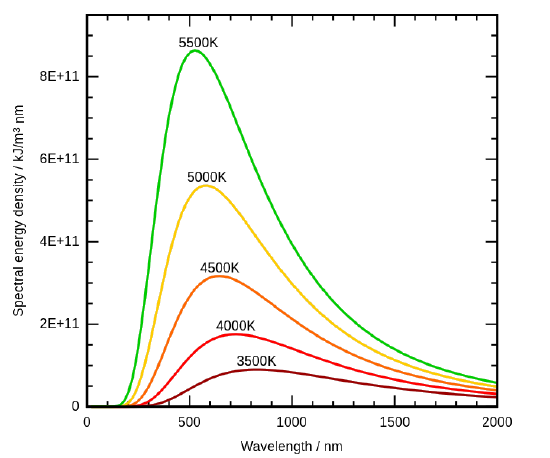
Durch Messung der Schwarzkörper-Emissionskurven bei verschiedenen Temperaturen (Abbildung \(\PageIndex{3}\)) konnten sie auch zwei wichtige phänomenologische Gesetze (d.h., formuliert aus experimentellen Beobachtungen, nicht aus Grundprinzipien der Natur): Das Stefan-Boltmann’sche Gesetz und das Wien’sche Verschiebungsgesetz.
Nicht alle Strahler sind Schwarzkörperstrahler
Die Strahlung eines Schwarzkörperstrahlers wird durch die thermische Aktivität des Materials erzeugt, nicht durch die Art des Materials oder wie es thermisch angeregt wurde. Einige Beispiele für Schwarze Körper sind Glühbirnen, Sterne und heiße Herdplatten. Die Emission erscheint als ein kontinuierliches Spektrum (Abbildung \(\PageIndex{3}\)) mit mehreren nebeneinander existierenden Farben. Allerdings ist nicht jeder Strahler ein Schwarzkörperstrahler. Zum Beispiel ist die Emission einer Fluoreszenzlampe kein solcher. Das folgende Spektrum zeigt die Verteilung des Lichts einer Fluoreszenzlampe und ist eine Mischung aus diskreten Banden bei verschiedenen Wellenlängen des Lichts im Gegensatz zu den kontinuierlichen Spektren in Abbildung \(\PageIndex{3}\) für Schwarzkörperstrahler.
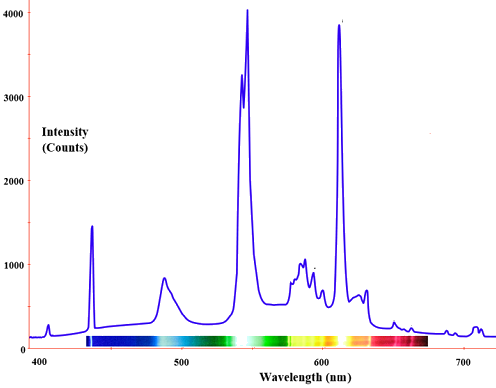
Fluoreszierende Glühbirnen enthalten eine Mischung aus Edelgasen (meist Argon und Neon) zusammen mit einem Tropfen Quecksilber bei niedrigem Druck. Eine unterschiedliche Mischung von sichtbaren Farben mischt sich, um ein Licht zu erzeugen, das uns weiß mit verschiedenen Schattierungen erscheint.
Das Stefan-Boltzmann-Gesetz
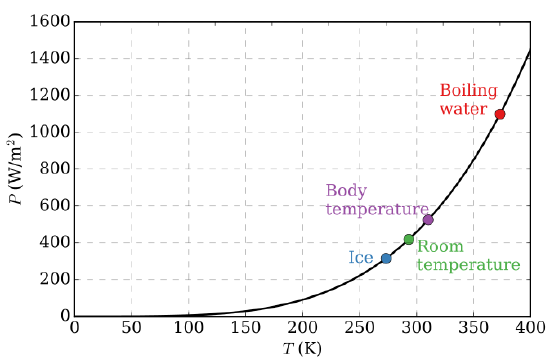
Die erste quantitative Vermutung, die auf experimentellen Beobachtungen beruhte, war das Stefan-Boltzmann-Gesetz (1879), das besagt, dass die Gesamtleistung (d.h., integriert über alle emittierenden Frequenzen in Abbildung \(\PageIndex{3}\)), die von einem Quadratmeter schwarzer Oberfläche abgestrahlt wird, mit der vierten Potenz der absoluten Temperatur (Abbildung \(\PageIndex{4}\)) steigt:
\
wobei
- \(P\) ist die Gesamtmenge der von einem Objekt pro Quadratmeter emittierten Strahlung (\(Watt\; m^{-2}\))
- \(\sigma\) ist eine Konstante, die Stefan-Boltzman-Konstante (\(5.67 \times 10^{-8}\, Watts\; m^{-2} K^{-4}\))
- \(T\) ist die absolute Temperatur des Objekts (in K)
Das Stefan-Boltzmann-Gesetz lässt sich leicht beobachten, indem man den integrierten Wert (d.h., unter den Kurven) der experimentellen Schwarzkörperstrahlungsverteilung in Abbildung \(\PageIndex{3}\) bei verschiedenen Temperaturen. 1884 leitete Boltzmann dieses \(T^4\)-Verhalten aus der Theorie ab, indem er klassische thermodynamische Überlegungen auf einen mit elektromagnetischer Strahlung gefüllten Kasten anwandte und die Maxwellschen Gleichungen verwendete, um Druck und Energiedichte in Beziehung zu setzen. Das heißt, die winzige Energiemenge, die aus dem Loch herauskommt (Abbildung \(\PageIndex{2}\)), würde natürlich die gleiche Temperaturabhängigkeit haben wie die Strahlungsintensität im Inneren.
Beispiel \(\PageIndex{1}\)
Die Oberflächentemperatur der Sonne beträgt 5700 K.
- Wie viel Energie wird von der Sonne abgestrahlt?
- Gegeben, dass der Abstand zur Erde etwa 200 Sonnenradien beträgt, wie groß ist die maximal mögliche Leistung einer ein Quadratkilometer großen Solaranlage?
Lösung
(a) Zuerst berechnen wir die Fläche der Sonne und dann den Fluss (Leistung). Die Sonne hat einen Radius von \( 6,96 \times 10^{8} m \)
Die Fläche der Sonne beträgt \( A = 4 \pi R^{2} \).
&= 6.08 \times 10^{18} m^2 \end{align*}\]
Die von der Sonne abgestrahlte Leistung (über das Stefan-Boltzmann-Gesetz) ist \(P = \sigma T^{4} \).
&= 5,98 \times 10^{7} Watt/m^2 \end{align*}\]
Dieser Wert gilt pro Quadratmeter.
(b) Die von der Sonne abgestrahlte Gesamtleistung berechnet sich so:
&= 3,6 \Times 10^{26} Watt \end{align*}\]
Wien’s Verdrängungsgesetz
Die zweite phänomenologische Beobachtung aus dem Experiment war das Wien’sche Verdrängungsgesetz. Das Wien’sche Gesetz identifiziert die dominante (Spitzen-)Wellenlänge oder Farbe des Lichts, das von einem Körper bei einer bestimmten Temperatur ausgeht. Wenn die Ofentemperatur variiert, ändert sich auch die Frequenz, bei der die emittierte Strahlung am intensivsten ist (Abbildung \(\PageIndex{3}\)). Tatsächlich ist diese Frequenz direkt proportional zur absoluten Temperatur:
\
wobei die Proportionalitätskonstante \(5,879 \times 10^{10} Hz/K\) beträgt.
Wien selbst hat dieses Gesetz 1893 theoretisch hergeleitet, indem er Boltzmanns thermodynamischen Überlegungen folgte. Zuvor war es, zumindest halbquantitativ, von einem amerikanischen Astronomen, Langley, beobachtet worden. Diese Verschiebung von \(\nu_{max}\) mit \(T\) nach oben ist jedem bekannt – wenn ein Eisen in einem Feuer erhitzt wird (Abbildung \(\PageIndex{1}\)), ist die erste sichtbare Strahlung (bei etwa 900 K) tiefrot, das niedrigste sichtbare Licht der Frequenz. Bei weiterem Anstieg von \(T\) ändert sich die Farbe zu Orange, dann zu Gelb und schließlich zu Blau bei sehr hohen Temperaturen (10.000 K oder mehr), bei denen die Spitze der Strahlungsintensität über das Sichtbare hinaus ins Ultraviolette gewandert ist.
Eine andere Darstellung des Wien’schen Gesetzes (Gleichung \(\ref{Eq2}\)) in Bezug auf die Spitzenwellenlänge des Lichts ist
\
wobei \(T\) die absolute Temperatur in Kelvin und \(b\) eine Proportionalitätskonstante ist, die Wien’sche Verschiebungskonstante genannt wird, gleich \(2.89 \mal 10^{-3} m\, K\), oder bequemer, um die Wellenlänge in Mikrometern zu erhalten, \(b≈2900\; μm \cdot K\). Dies ist eine inverse Beziehung zwischen Wellenlänge und Temperatur. Je höher also die Temperatur ist, desto kürzer bzw. kleiner ist die Wellenlänge der Wärmestrahlung. Je niedriger die Temperatur, desto länger bzw. größer ist die Wellenlänge der Wärmestrahlung. Bei sichtbarer Strahlung emittieren heiße Objekte blaueres Licht als kühle Objekte.
Beispiel \(\PageIndex{2}\)
Wenn die Körperoberflächentemperatur 90 °F beträgt.
- Wie viel Strahlungsenergie in \(W\, m^{-2}\) würde Ihr Körper emittieren?
- Wie groß ist die Spitzenwellenlänge der emittierten Strahlung?
- Wie hoch ist die gesamte von Ihrem Körper emittierte Strahlungsenergie in Watt? Hinweis: Der durchschnittliche erwachsene menschliche Mann hat eine Körperoberfläche von etwa 1,9 \(m^2\) und die durchschnittliche Körperoberfläche einer Frau beträgt etwa 1,6 \(m^2\).
Lösung
(a) 90 °F sind 305 K. Wir verwenden das Stefan-Boltzmann-Gesetz (Gleichung \ref{Eq1}. Die Gesamtmenge der emittierten Strahlung beträgt \( P = \sigma T^4 \).
\ &= 491 W\, m^{-2} \end{align*}\]
Die Spitzenwellenlänge der emittierten Strahlung wird mit Hilfe des Wienschen Gesetzes gefunden:
\ &= \frac{ 2.898 \times 10^{-3} m \cdot K}{305 K} \\ &= 9,5 \times 10^{-6} m = 9,5 \mu m\end{align*}}]
Die gesamte Strahlungsenergiedichte in Watt ist :
\text{Energie}_{\text{female}} &= (491 W\, m^{-2})(1,6 m^{2}) = 786 W \end{align*}\]
Beispiel \(\PageIndex{3}\): Die Temperatur der Sonne
Wie groß ist die Wellenlänge der maximalen Intensität der Sonnenstrahlung, wenn die Sonne beispielsweise eine Oberflächentemperatur von 5700 K hat?
Lösung
Wenn wir 5700 K für \(T\) in Gleichung \(\ref{Eq2a}\) einsetzen, erhalten wir
&= 5,1 \times 10^{-7} \end{align*}\]
Wenn wir wissen, dass violettes Licht eine Wellenlänge von etwa \(4,0 \times 10^{-7}\) Metern hat, gelbes Licht etwa \(5,6 \times 10^{-7}\) Meter und rotes Licht etwa \(6,6 \times 10^{-7}\) Meter, was können wir dann über die Farbe der Spitzenstrahlung der Sonne sagen? Die Spitzenwellenlänge der Sonnenstrahlung liegt bei einer etwas kürzeren Wellenlänge als die Farbe Gelb, daher ist sie leicht grünlich gelb. Um diese grünliche Färbung der Sonne zu sehen, müsste man sie aus dem Weltraum betrachten. Es stellt sich heraus, dass die Erdatmosphäre einige der kürzeren Wellen des Sonnenlichts streut, wodurch sich die Spitzenwellenlänge zu reinem Gelb verschiebt.
Erinnern Sie sich daran, dass sich Wärmestrahlung immer über einen breiten Wellenlängenbereich erstreckt (Abbildung \(\PageIndex{2}\)) und Gleichung \ref{Eq2a} nur die einzelne Wellenlänge angibt, die die Spitze des Spektrums darstellt. Obwohl die Sonne also gelblich-weiß erscheint, sieht man, wenn man das Sonnenlicht mit einem Prisma zerstreut, Strahlung mit allen Farben des Regenbogens. Gelb stellt nur eine charakteristische Wellenlänge der Emission dar.
Übung \(\PageIndex{1}\)
- Bei welcher Wellenlänge gibt die Sonne den größten Teil ihrer Strahlung ab, wenn sie eine Temperatur von 5.778 K hat?
- Bei welcher Wellenlänge gibt die Erde die meiste Strahlung ab, wenn sie eine Temperatur von 288 K hat?
Antwort a
500 nm
Antwort b
10,0 Mikrometer
Das Rayleigh-Jeans-Gesetz
Lord Rayleigh und J. H. Jeans entwickelten eine Gleichung, die die Schwarzkörperstrahlung bei niedrigen Frequenzen erklärte. Die Gleichung, die die Schwarzkörperstrahlung zu erklären schien, basierte auf allen damals bekannten Annahmen der Physik. Die große Annahme, die Rayleigh und Jeans aufstellten, war, dass dem System kontinuierlich infinitesimale Energiemengen zugeführt wurden, wenn die Frequenz erhöht wurde. Die klassische Physik ging davon aus, dass die von Atomschwingungen emittierte Energie einen beliebigen kontinuierlichen Wert haben kann. Dies galt für alles, was bis zu diesem Zeitpunkt untersucht worden war, einschließlich Dingen wie Beschleunigung, Position oder Energie. Ihr daraus resultierendes Rayleigh-Jeans-Gesetz war
&= \dfrac{8 \pi k_B T}{c^3} \nu^2 d\nu \label{Eq3} \end{align}\]
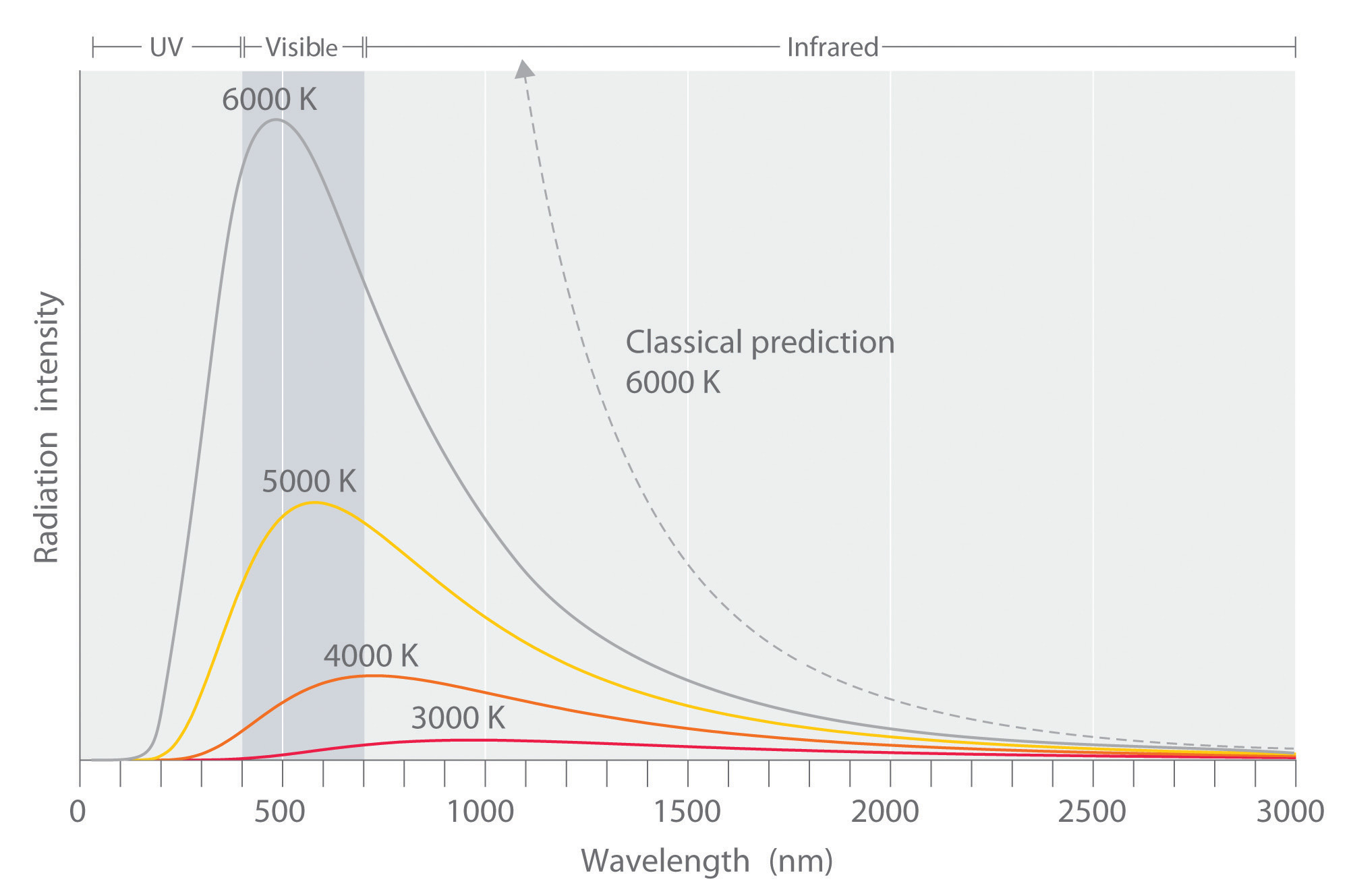
Experimentelle Daten, die an der Black Box durchgeführt wurden, zeigten etwas andere Ergebnisse als die, die durch das Rayleigh-Jeans-Gesetz (Abbildung \(\PageIndex{5}\)) erwartet wurden. Das Gesetz war von vielen Physikern der damaligen Zeit untersucht und weithin akzeptiert worden, aber die experimentellen Ergebnisse logen nicht, etwas war anders zwischen dem, was theoretisiert wurde und dem, was tatsächlich passiert. Die experimentellen Ergebnisse zeigten eine glockenförmige Kurve, aber nach dem Rayleigh-Jeans-Gesetz divergierte die Frequenz, wenn sie sich dem ultravioletten Bereich näherte (Gleichung \(\ref{Eq3}\)). Ehrenfest nannte dies später die „ultraviolette Katastrophe“.
Es ist wichtig zu betonen, dass Gleichung \(\ref{Eq3}\) ein klassisches Ergebnis ist: die einzigen Eingaben sind die klassische Dynamik und die elektromagnetische Theorie von Maxwell. Die Ladung \(e\) des Oszillators taucht nicht auf: Das Ergebnis ist unabhängig von der Kopplungsstärke zwischen dem Oszillator und der Strahlung, die Kopplung muss nur stark genug sein, um ein thermisches Gleichgewicht zu gewährleisten. Die Herleitung des Gesetzes ist hier zu finden.
Differentielle vs. integrale Darstellung der Verteilung
Strahlung wird als kontinuierliche Verteilung der Amplitude gegen die Wellenlänge oder, äquivalent, gegen die Frequenz verstanden (Abbildung \(\PageIndex{5}\)). Bei einer bestimmten Frequenz \(\nu\) ist die Strahlung nach dem Rayleigh-Jeans-Gesetz
In der Praxis ist es schwierig, eine einzelne Frequenz zu messen, und wir sind eher an Frequenzintervallen interessiert. Eine exakte Frequenz ist der Grenzwert einer Folge von immer kleineren Intervallen. Wenn wir die Annahme treffen, dass für ein hinreichend kleines Intervall \(ρ(\nu,T)\) nicht variiert, erhalten wir Ihre Definition für das Differential \(dρ(ν,T)\) in Gleichung \ref{Eq3}:
Die Annahme ist aufgrund der Stetigkeit von \(ρ(\nu,T)\) gerecht. Dies ist die Approximation eines Integrals auf einem sehr kleinen Intervall \(d\nu\) durch die Höhe eines Punktes in diesem Intervall (\(\frac{8\pi k_bT\nu^2}{c^3}\)) mal seine Länge (\(d\nu\)). Wenn wir also eine unendliche Menge von kleinen Intervallen wie das obige summieren, erhalten wir ein Integral. Die Gesamtstrahlung zwischen \(\nu_1\) und \(\nu_2\) wird sein:
Beachten Sie, dass \(ρ(\nu,T)\) quadratisch in \(\nu\) ist.
Beispiel \(\PageIndex{4}\): die Ultraviolett-Katastrophe
Wie groß ist die gesamte spektrale Strahldichte eines Strahlers, der für sein Emissionsspektrum dem Rayleigh-Jeans-Gesetz folgt?
Lösung
Die gesamte spektrale Strahldichte \(\rho_{tot}(T)\) ist die kombinierte Emission über alle möglichen Wellenlängen (oder äquivalent, Frequenzen), die ein Integral über die entsprechende Verteilung ist (Gleichung \ref{Eq3} für das Rayleigh-Jeans-Gesetz).
&= \int_0^\infty \dfrac{8 \pi k_B T}{c^3} \nu^2 d\nu \end{align*}\]
Aber das Integral
\
konvergiert nicht. Schlimmer noch, es ist unendlich,
Das klassisch abgeleitete Rayleigh-Jeans-Gesetz sagt also voraus, dass die Strahldichte eines Schwarzen Körpers unendlich ist. Da die Strahldichte die Leistung pro Winkel und Flächeneinheit ist, impliziert dies auch, dass die Gesamtleistung und damit die Energie, die ein Schwarzer Strahler abgibt, unendlich ist, was offenkundig absurd ist. Dies wird als Ultraviolett-Katastrophe bezeichnet, weil die absurde Vorhersage dadurch verursacht wird, dass das klassische Gesetz das Verhalten bei hohen Frequenzen/kleinen Wellenlängen nicht korrekt vorhersagt (Abbildung \(\PageIndex{5}\)).
Beitragende
-
Michael Fowler (Beams Professor, Department of Physics, University of Virginia)
-
David M. Hanson, Erica Harvey, Robert Sweeney, Theresa Julia Zielinski („Quantenzustände von Atomen und Molekülen“)
-
Paul Flowers (University of North Carolina – Pembroke), Klaus Theopold (University of Delaware) und Richard Langley (Stephen F. Austin State University) sind mitwirkende Autoren. Die Lehrbuchinhalte wurden von OpenStax College produziert und stehen unter einer Creative Commons Attribution License 4.0 Lizenz. Kostenloser Download unter http://cnx.org/contents/85abf193-2bd…[email protected]).
- ACuriousMind (StackExchange)