La formule de la vitesse moyenne est utilisée pour trouver le taux uniforme qui implique que quelque chose se déplace à un rythme fixe et régulier.
Par exemple, une voiture voyage pendant 3 heures. Elle parcourt 30 miles dans la première heure, 45 miles dans la deuxième heure et 75 miles dans la troisième heure.
Vitesse à la première heure = 30 miles / heure
Vitesse à la deuxième heure = 45 miles / heure
Vitesse à la troisième heure = 75 miles / heure
Nous avons trois vitesses différentes au cours du trajet de trois heures.
Si nous voulons trouver la vitesse moyenne pour l’ensemble du trajet de trois heures, nous devons trouver le rapport entre la distance totale parcourue et le temps total mis.
C’est-à-dire , vitesse constante = (30 + 45 + 75) / 3
= 150 / 3
= 50 miles / heure
Sur la base de l’exemple ci-dessus, la formule permettant de trouver la vitesse moyenne est donnée ci-dessous.
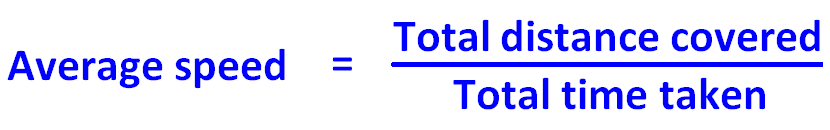
Si une personne se rend de A à B à une certaine vitesse, disons « x » miles par heure. Elle revient de B à A à une vitesse différente, disons « y » miles par heure. Dans les deux sens, il parcourt la même distance, mais à des vitesses différentes.
Alors, la formule est pour trouver la vitesse moyenne pour tout le trajet est donnée ci-dessous.
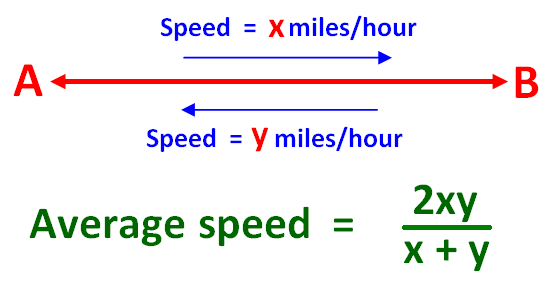
Formule de la vitesse moyenne – Exemples
Exemple 1 :
David a roulé pendant 3 heures à un rythme de 50 miles par heure, pendant 2 heures à 60 miles par heure et pendant 5 heures à un rythme de 70 miles par heure. Quelle a été sa vitesse moyenne sur l’ensemble du trajet ?
Réponse :
Etape 1 :
La formule de la vitesse moyenne est
= Distance totale / Temps total mis.
Et aussi, la formule pour la distance est
= Vitesse ⋅ Temps
Etape 2 :
La distance parcourue au cours des 3 premières heures est
= 50 ⋅ 3
= 150 miles
Distance parcourue dans les 2 prochaines heures est
= 60 ⋅ 2
= 120 miles
Distance parcourue dans les 5 dernières heures est
= 70 ⋅ 5
= 350 miles
Étape 3 :
Alors, la distance totale est
= 150 + 120 + 350
= 620 miles
.
Le temps total est
= 3 + 2 + 5
= 10 heures
Étape 4 :
Donc, la vitesse moyenne est
= 620 / 10
= 62
Donc, la vitesse moyenne pour tout le trajet est de 62 miles par heure.
Exemple 2 :
Jose voyage du lieu A au lieu B à une certaine vitesse. Lorsqu’il revient du lieu B au lieu A, sa vitesse est de 60 miles par heure.Si la vitesse moyenne pour l’ensemble du trajet est de 72 miles par heure, trouvez sa vitesse lorsqu’il se rend du lieu A au lieu B.
Réponse :
Étape 1 :
Détendez « a » la vitesse du lieu A au lieu B.
Vitesse du lieu B au lieu A = 60 miles/heure
Étape 2 :
Ici, dans les deux sens, il parcourt la même distance.
Alors, la formule pour trouver la vitesse moyenne est
= 2xy / (x + y)
Étape 3 :
x —-> Vitesse du lieu A à B
x = a
y —-> Vitesse du lieu B au lieu A
y = 60
Etape 4 :
Donné : la vitesse moyenne est de 72 miles/heure.
(2 ⋅ a ⋅ 60) / (a + 60) = 72
120a = 72(a + 60)
120a. = 72a + 4320
48a = 4320
a = 90
So, la vitesse du lieu A au lieu B est de 90 miles par heure.
Exemple 3 :
David voyage du lieu A au lieu B à une certaine vitesse. Lorsqu’il revient du lieu B au lieu A, il augmente sa vitesse 2 fois. Si la vitesse constante pendant tout le trajet est de 80 miles par heure, trouvez sa vitesse lorsqu’il se rend du lieu A au lieu B.
Réponse :
Étape 1 :
Disons que « a » est la vitesse du lieu A au lieu B.
Alors, vitesse du lieu B vers A = 2a
Étape 2 :
La distance parcourue dans les deux sens (A vers B et B vers A) est la même.
Donc, la formule pour trouver la vitesse moyenne est
= 2xy / (x + y)
Etape 3 :
x —-> Vitesse du lieu A à B
x = a
y —-> Vitesse du lieu B au lieu A
y = 2a
Etape 4 :
Donné : Vitesse moyenne = 80 miles/heure
(2 ⋅ a ⋅ 2a) / (a + 2a) = 80
4a². / 3a = 80
4a / 3 = 80
a = 60
So, la vitesse du lieu A au lieu B est de 60 miles par heure.
Exemple 4 :
Une personne met 5 heures pour aller du lieu A au lieu B à la vitesse de 40 miles par heure. Il revient du lieu B au lieu A avec une vitesse accrue de 25%. Trouvez la vitesse moyenne pour l’ensemble du trajet.
Réponse :
Etape 1 :
Vitesse ( de A à B ) = 40 miles/heure
Vitesse ( de B à A ) = 50 miles/heure (25% d’augmentation)
Etape 2 :
La distance parcourue dans les deux sens (A vers B et B vers A) est la même.
Donc, la formule pour trouver la distance moyenne est
= 2xy / (x + y)
Etape 3 :
x —-> Vitesse du lieu A à B
x = 40
y —-> Vitesse du lieu B au lieu A
y = 50
Etape 4 :
Vitesse moyenne = (2 ⋅ 40 ⋅ 50) / (40 + 50)
Vitesse moyenne = 44.44
Donc, la vitesse moyenne pour l’ensemble du trajet est d’environ 44,44 miles/heure.
Exemple 5 :
Vitesse ( A à B ) = 20 miles/heure,
Vitesse (B à C ) = 15 miles/heure,
Vitesse (C à D ) = 30 miles/heure
Si les distances de A à B, B à C et C à D sont égales et qu’il faut 3 heures pour aller de A à B, trouvez la vitesse moyenne de A à D.
Réponse :
Étape 1 :
La formule pour trouver la distance est
= Taux ⋅ Temps
La distance de A à B est
= 20 ⋅ 3
= 60 miles
Donnée : Les distances de A à B, de B à C et de C à D sont égales.
La distance totale de A à D est
= 60 + 60 + 60
= 180 miles
Étape 2 :
La formule pour trouver le temps est
= Distance / Vitesse
.
Temps (A à B) = 60 / 20 = 3 heures
Temps (B à C) = 60 / 15 = 4 heures
Temps (C à D) = 60 / 30 = 2 heures
Temps total mis pour passer de A à D est
= 3 + 4 + 2
= 9 heures
Étape 3 :
La formule pour trouver la vitesse moyenne est
= Distance totale / Temps total. temps
= 180 / 9
= 20
So, la vitesse moyenne de A à D est de 20 miles par heure.

Pour avoir plus de problèmes sur la vitesse moyenne,
Veuillez cliquer ici
A part les trucs donnés ci-dessus, si vous avez besoin d’autres trucs, veuillez utiliser notre recherche personnalisée google ici.
Si vous avez des commentaires sur notre contenu mathématique, veuillez nous envoyer un mail :
Nous apprécions toujours vos commentaires.
Vous pouvez également visiter les pages web suivantes sur différentes choses en mathématiques.
PROBLEMES DE MOTS
Problèmes de mots HCF et LCM
Problèmes de mots sur les équations simples
Problèmes de mots sur les équations linéaires
Problèmes de mots sur les équations quadratiques
.
Des problèmes d’algèbre
Des problèmes de mots sur les trains
Des problèmes d’aire et de périmètre
Des problèmes de mots sur la variation directe et la variation inverse
Des problèmes de mots sur . prix unitaire
Des problèmes de mots sur le taux unitaire
Des problèmes de mots sur la comparaison des taux
Des problèmes de mots sur la conversion des unités coutumières
Des problèmes de mots sur la conversion des unités métriques
Des problèmes de mots sur l’intérêt simple. intérêts
Des problèmes de mots sur les intérêts composés
Des problèmes de mots sur les types d’angles
Des problèmes de mots sur les angles complémentaires et supplémentaires
Des problèmes de mots sur les faits doubles
.
Des problèmes de mots sur la trigonométrie
Des problèmes de mots sur le pourcentage
Des problèmes de mots sur les profits et les pertes
Des problèmes de mots sur le balisage et la démarque
Des problèmes de mots sur les décimales
Des problèmes de mots sur les fractions
.
Des problèmes écrits sur les fractrions mixtes
Des problèmes écrits sur les équations à une étape
Des problèmes écrits sur les inégalités linéaires
Des problèmes écrits sur les rapports et les proportions
Des problèmes écrits sur le temps et le travail
Des problèmes écrits sur . ensembles et diagrammes de Venn
Des problèmes verbaux sur les âges
Des problèmes verbaux sur le théorème de Pythagore
Des problèmes verbaux sur le pourcentage d’un nombre
Des problèmes verbaux sur la vitesse constante
Des problèmes verbaux sur la vitesse moyenne
.
Des problèmes de mots sur la somme des angles d’un triangle est de 180 degrés
D’AUTRES SUJETS
Des raccourcis sur les pertes et profits
Des raccourcis sur les pourcentages
Des raccourcis sur les tables de temps
Des raccourcis sur le temps, vitesse et distance raccourcis
Rapport et proportion raccourcis
Domaine et étendue des fonctions rationnelles
Domaine et étendue des fonctions rationnelles à trous
Graphie des fonctions rationnelles
.
Graphie des fonctions rationnelles à trous
Conversion des décimaux répétitifs en fractions
Représentation décimale des nombres rationnels
Retrouver la racine carrée en utilisant la division longue
L.C.M pour résoudre des problèmes de temps et de travail
Traduction des problèmes verbaux en expressions algébriques
Remainde lorsque 2 puissance 256 est divisé par 17
Remainde lorsque 17 puissance 23 est… divisée par 16
Somme de tous les nombres à trois chiffres divisibles par 6
Somme de tous les nombres à trois chiffres divisibles par 7
Somme de tous les nombres à trois chiffres divisibles par 8
Somme de tous les nombres à trois chiffres formés à l’aide de 1, 3, 4
Somme des trois nombres à quatre chiffres formés avec des chiffres non nuls
Somme des trois nombres à quatre chiffres formés en utilisant 0, 1, 2, 3
Somme des trois nombres à quatre chiffres formés en utilisant 1, 2, 5, 6
.