Obiettivi di apprendimento
Un fenomeno sperimentale che non poteva essere adeguatamente spiegato dalla fisica classica era la radiazione del corpo nero. Gli obiettivi di questa sezione includono
- Avere familiarità con i radiatori di corpo nero
- Applicare la legge di Stefan-Boltmann per stimare l’emissione totale di luce da un radiatore
- Applicare la legge dello spostamento di Wien per stimare la lunghezza d’onda di picco (o frequenza) dell’emissione da un radiatore di corpo nero
- Comprendere la legge di Rayleigh-Jeans e come non riesce a modellare correttamente la radiazione di corpo nero
Tutta la materia normale a temperature superiori allo zero assoluto emette radiazione elettromagnetica, che rappresenta una conversione dell’energia termica interna di un corpo in energia elettromagnetica, ed è quindi chiamata radiazione termica. Al contrario, tutta la materia normale assorbe in qualche misura la radiazione elettromagnetica. Un oggetto che assorbe TUTTE le radiazioni che gli cadono addosso, a tutte le lunghezze d’onda, è chiamato corpo nero. Quando un corpo nero è ad una temperatura uniforme, la sua emissione ha una distribuzione di frequenza caratteristica che dipende dalla temperatura. Questa emissione è chiamata radiazione di corpo nero.
Un corpo nero a temperatura ambiente appare nero, poiché la maggior parte dell’energia che irradia è infrarossa e non può essere percepita dall’occhio umano. Poiché l’occhio umano non può percepire le onde luminose a frequenze più basse, un corpo nero, visto al buio alla temperatura più bassa appena visibile, appare soggettivamente grigio, anche se il suo spettro fisico oggettivo ha un picco nella gamma degli infrarossi. Quando diventa un po’ più caldo, appare rosso spento. Man mano che la sua temperatura aumenta ulteriormente, diventa giallo, bianco e infine bianco-blu.

La radiazione del corpo nero ha uno spettro di frequenza caratteristico e continuo che sperimentalmente dipende solo dalla temperatura del corpo. In realtà, possiamo essere molto più precisi:
Un corpo emette radiazioni a una data temperatura e frequenza esattamente come assorbe la stessa radiazione.
Questa affermazione è stata dimostrata da Gustav Kirchhoff: il punto essenziale è che se invece supponiamo che un particolare corpo possa assorbire meglio di quanto emetta, allora in una stanza piena di oggetti tutti alla stessa temperatura, esso assorbirà le radiazioni degli altri corpi meglio di quanto irradi energia verso di loro. Questo significa che diventerà più caldo, e il resto della stanza diventerà più freddo, contraddicendo la seconda legge della termodinamica. Quindi, un corpo deve emettere radiazioni esattamente come assorbe la stessa radiazione ad una data temperatura e frequenza per non violare la seconda legge della termodinamica.
Ogni corpo a qualsiasi temperatura sopra lo zero assoluto irradierà in qualche misura, l’intensità e la distribuzione di frequenza della radiazione dipendono dalla struttura dettagliata del corpo. Per iniziare ad analizzare la radiazione di calore, dobbiamo essere specifici sul corpo che irradia: il caso più semplice possibile è un corpo idealizzato che è un perfetto assorbitore, e quindi anche (dal ragionamento di cui sopra) un perfetto emettitore. Quindi, come si costruisce un assorbitore perfetto in laboratorio? Nel 1859 Kirchhoff ebbe una buona idea: un piccolo buco nel lato di una grande scatola è un eccellente assorbitore, poiché qualsiasi radiazione che passa attraverso il buco rimbalza all’interno, assorbendone molta ad ogni rimbalzo, e ha poche possibilità di uscire di nuovo. Quindi, possiamo fare questo al contrario: avere un forno con un piccolo buco sul lato, e presumibilmente la radiazione che esce dal buco è la migliore rappresentazione di un emettitore perfetto che possiamo trovare (Figura \PageIndex{2}).
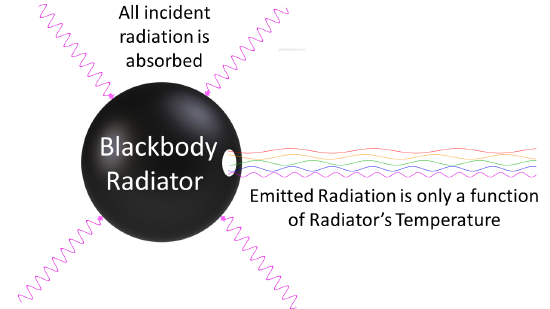
Negli anni 1890, le tecniche sperimentali erano migliorate a sufficienza da consentire di effettuare misure abbastanza precise della distribuzione di energia della radiazione di corpo nero. Nel 1895, all’Università di Berlino, Wien e Lummer praticarono un piccolo foro sul lato di un forno altrimenti completamente chiuso, e iniziarono a misurare la radiazione in uscita. Il fascio che usciva dal foro veniva fatto passare attraverso un reticolo di diffrazione, che inviava le diverse lunghezze d’onda/frequenze in diverse direzioni, tutte verso uno schermo. Un rilevatore veniva spostato su e giù lungo lo schermo per trovare quanta energia radiante veniva emessa in ogni gamma di frequenza. Hanno trovato una curva di intensità di radiazione/frequenza vicina alle distribuzioni della Figura \(\PageIndex{3}\).
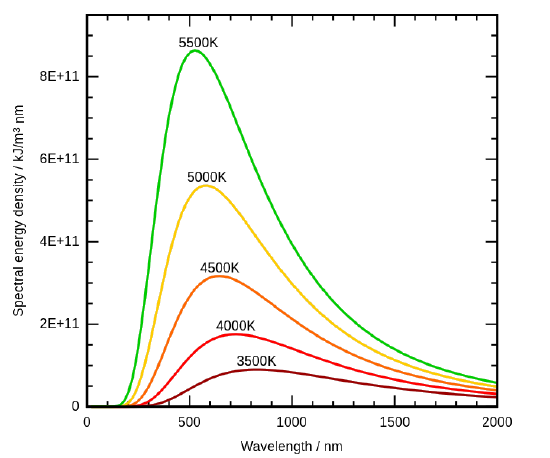
Misurando le curve di emissione del corpo nero a diverse temperature (Figura \(\PageIndex{3}\)), sono stati anche in grado di costruire due importanti leggi fenomenologiche (cioè, formulate da osservazioni sperimentali, non da principi fondamentali della natura): La legge di Stefan-Boltmann e la legge di Wien sullo spostamento.
Non tutti i radiatori sono radiatori a corpo nero
La radiazione di un radiatore a corpo nero è prodotta dall’attività termica del materiale, non dalla natura del materiale, né da come è stato eccitato termicamente. Alcuni esempi di corpi neri includono le lampadine a incandescenza, le stelle e i fornelli caldi. L’emissione appare come uno spettro continuo (Figura \PageIndex{3}) con più colori coesistenti. Tuttavia, non tutti i radiatori sono radiatori a corpo nero. Per esempio, l’emissione di una lampadina a fluorescenza non lo è. Il seguente spettro mostra la distribuzione della luce da un tubo luminoso a fluorescenza ed è una miscela di bande discrete a diverse lunghezze d’onda della luce in contrasto con gli spettri continui in Figura \(\PageIndex{3}) per i radiatori a corpo nero.
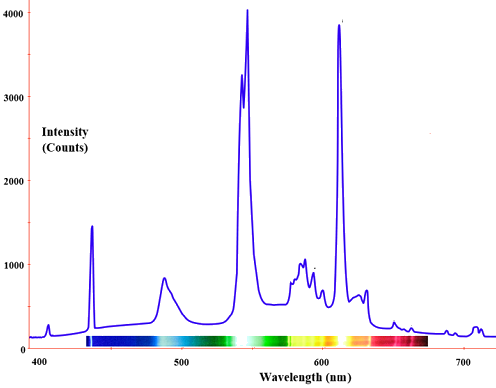
Le lampadine fluorescenti contengono una miscela di gas inerti (solitamente argon e neon) insieme ad una goccia di mercurio a bassa pressione. Un diverso mix di colori visibili si fonde per produrre una luce che ci appare bianca con diverse sfumature.
La legge di Stefan-Boltzmann
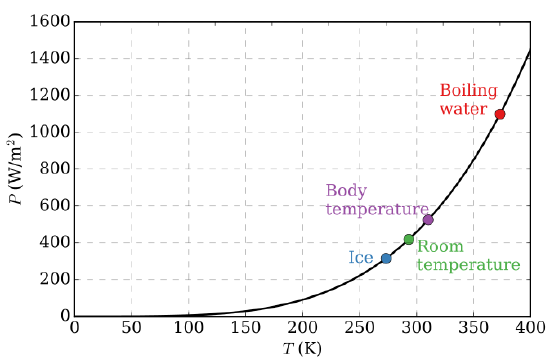
La prima congettura quantitativa basata su osservazioni sperimentali fu la legge di Stefan-Boltzmann (1879) che afferma la potenza totale (cioè, integrata su tutte le frequenze di emissione nella Figura \PageIndex{3})) irradiata da un metro quadrato di superficie nera va come la quarta potenza della temperatura assoluta (Figura \PageIndex{4}):
dove
- (P) è la quantità totale di radiazione emessa da un oggetto per metro quadrato (\(Watts\; m^{-2}))
- (\sigma\) è una costante chiamata costante di Stefan-Boltzman (\(5.67 \volte 10^{-8}, Watts\; m^{-2} K^{-4}))
- (T\) è la temperatura assoluta dell’oggetto (in K)
La legge di Stefan-Boltzmann è facilmente osservabile confrontando il valore integrato (cioè, sotto le curve) della distribuzione sperimentale della radiazione di corpo nero nella figura \(\PageIndex{3}\) a diverse temperature. Nel 1884, Boltzmann ha derivato questo comportamento \T^4\ dalla teoria applicando il ragionamento termodinamico classico ad una scatola riempita di radiazione elettromagnetica, usando le equazioni di Maxwell per mettere in relazione la pressione con la densità di energia. Cioè, la piccola quantità di energia che esce dal buco (figura \(\PageIndex{2})) avrebbe naturalmente la stessa dipendenza dalla temperatura dell’intensità della radiazione all’interno.
Esempio \(\PageIndex{1})
La temperatura superficiale del sole è 5700 K.
- Quanta energia viene irradiata dal sole?
- Posto che la distanza dalla terra è di circa 200 raggi solari, qual è la massima potenza possibile da un’installazione di energia solare di un chilometro quadrato?
Soluzione
(a) Prima calcoliamo l’area del sole seguita dal flusso (potenza). Il sole ha un raggio di \( 6.96 \volte 10^{8} m \)
L’area del sole è \( A = 4 \pi R^{2} \).
&= 6.08 volte 10^{18} m^2 \end{align*}]
La potenza irradiata dal sole (attraverso la legge di Stefan-Boltzmann) è \(P = \sigma T^{4} \).
&= 5,98 volte 10^{7} Watts/m^2 \end{align*}}]
Questo valore è per metro quadrato.
(b) Per calcolare la potenza totale irradiata dal sole è così:
&= 3,6 \volte 10^{26} Watts \end{align*}]
La legge di spostamento di Wien
La seconda osservazione fenomenologica dell’esperimento è la legge di spostamento di Wien. La legge di Wien identifica la lunghezza d’onda dominante (picco), o colore, della luce proveniente da un corpo ad una data temperatura. Al variare della temperatura del forno, varia anche la frequenza alla quale la radiazione emessa è più intensa (Figura \PageIndex{3}). Infatti, questa frequenza è direttamente proporzionale alla temperatura assoluta:
dove la costante di proporzionalità è \(5,879 \volte 10^{10} Hz/K\).
Wien stesso dedusse questa legge teoricamente nel 1893, seguendo il ragionamento termodinamico di Boltzmann. Era stata precedentemente osservata, almeno semi-quantitativamente, da un astronomo americano, Langley. Questo spostamento verso l’alto di \nu_{max} con \T\ è familiare a tutti – quando un ferro viene riscaldato in un fuoco (Figura \PageIndex{1}), la prima radiazione visibile (a circa 900 K) è rosso intenso, la più bassa frequenza della luce visibile. Un ulteriore aumento di \(T\) fa sì che il colore cambi in arancione, poi in giallo e infine in blu a temperature molto alte (10.000 K o più) per le quali il picco di intensità della radiazione si è spostato oltre il visibile nell’ultravioletto.
Un’altra rappresentazione della legge di Wien (equazione \ref{Eq2}}) in termini di lunghezza d’onda di picco della luce è
dove \(T\) è la temperatura assoluta in kelvin e \(b\) è una costante di proporzionalità chiamata costante di spostamento di Wien, pari a \(2.89 volte 10^{-3} m\, K\), o più convenientemente per ottenere la lunghezza d’onda in micrometri, \(b≈2900\; μm \cdot K\). Questa è una relazione inversa tra lunghezza d’onda e temperatura. Quindi, più alta è la temperatura, più corta o piccola è la lunghezza d’onda della radiazione termica. Più bassa è la temperatura, più lunga o grande è la lunghezza d’onda della radiazione termica. Per la radiazione visibile, gli oggetti caldi emettono una luce più blu di quelli freddi.
Esempio \(\PageIndex{2}})
Se la temperatura corporea superficiale è 90 °F.
- Quanta energia radiante in \(W\, m^{-2}\ emette il tuo corpo?
- Qual è la lunghezza d’onda di picco della radiazione emessa?
- Qual è l’energia radiante totale emessa dal tuo corpo in Watt? Nota: Il maschio adulto medio ha una superficie corporea di circa 1,9 \(m^2\) e la superficie corporea media di una donna è di circa 1,6 \(m^2\).
Soluzione
(a) 90 °F sono 305 K. Usiamo la legge di Stefan-Boltzmann (equazione \ref{Eq1}. La quantità totale di radiazione emessa sarà \( P = \sigma T^4 \).
&= 491 W\, m^{-2} \end{align*}}]
La lunghezza d’onda di picco della radiazione emessa si trova usando la legge di Wien:
&= \frac{ 2.898 \volte 10^{-3} m \cdot K}{305 K} &= 9,5 \volte 10^{-6} m = 9,5 \mu m\end{align*}]
La densità totale di energia radiante in Watt è :
\testo{Energia}_{femmina}} &= (491 W, m^{-2})(1,6 m^{2}) = 786 W \end{align*}}]
Esempio \(\PageIndex{3}): La temperatura del Sole
Per esempio, se il Sole ha una temperatura superficiale di 5700 K, qual è la lunghezza d’onda di massima intensità della radiazione solare?
Soluzione
Se sostituiamo 5700 K per \(T\) nell’equazione \ref{Eq2a}}, abbiamo
&= 5.1 \volte 10^{-7}
Sapendo che la luce viola ha una lunghezza d’onda di circa \4,0 volte 10^{-7} metri, il giallo di circa \5,6 volte 10^{-7} metri, e il rosso di circa \6,6 volte 10^{-7} metri, cosa possiamo dire del colore della radiazione di picco del Sole? La lunghezza d’onda di picco della radiazione del Sole è ad una lunghezza d’onda leggermente più corta del colore giallo, quindi è un giallo leggermente verdastro. Per vedere questa sfumatura verdastra del Sole, bisognerebbe guardarlo dallo spazio. Si scopre che l’atmosfera terrestre disperde alcune delle onde più corte della luce solare, il che sposta la sua lunghezza d’onda di picco verso il giallo puro.
Ricorda che la radiazione termica si estende sempre su una vasta gamma di lunghezze d’onda (Figura \PageIndex{2}) e l’equazione \ref{Eq2a} specifica solo la singola lunghezza d’onda che è il picco dello spettro. Così, anche se il Sole appare bianco-giallastro, quando si disperde la luce del sole con un prisma si vede una radiazione con tutti i colori dell’arcobaleno. Il giallo rappresenta solo una lunghezza d’onda caratteristica dell’emissione.
Esercizio \(\PageIndex{1})
- A quale lunghezza d’onda il sole emette la maggior parte della sua radiazione se ha una temperatura di 5.778 K?
- A quale lunghezza d’onda la terra emette la maggior parte della sua radiazione se ha una temperatura di 288 K?
Risposta a
500 nm
Risposta b
10,0 micron
La legge di Rayleigh-Jeans
Lord Rayleigh e J. H. Jeans svilupparono un’equazione che spiegava la radiazione dei corpi neri alle basse frequenze. L’equazione che sembrava esprimere la radiazione di corpo nero era costruita su tutti i presupposti noti della fisica dell’epoca. La grande assunzione che Rayleigh e Jean implicava era che quantità infinitesimali di energia venivano continuamente aggiunte al sistema quando la frequenza veniva aumentata. La fisica classica presupponeva che l’energia emessa dalle oscillazioni atomiche potesse avere qualsiasi valore continuo. Questo era vero per tutto ciò che era stato studiato fino a quel momento, comprese cose come l’accelerazione, la posizione o l’energia. La loro risultante legge di Rayleigh-Jeans era
&= \dfrac{8 \pi k_B T}{c^3} \nu^2 d\nu \label{Eq3} \end{align}]
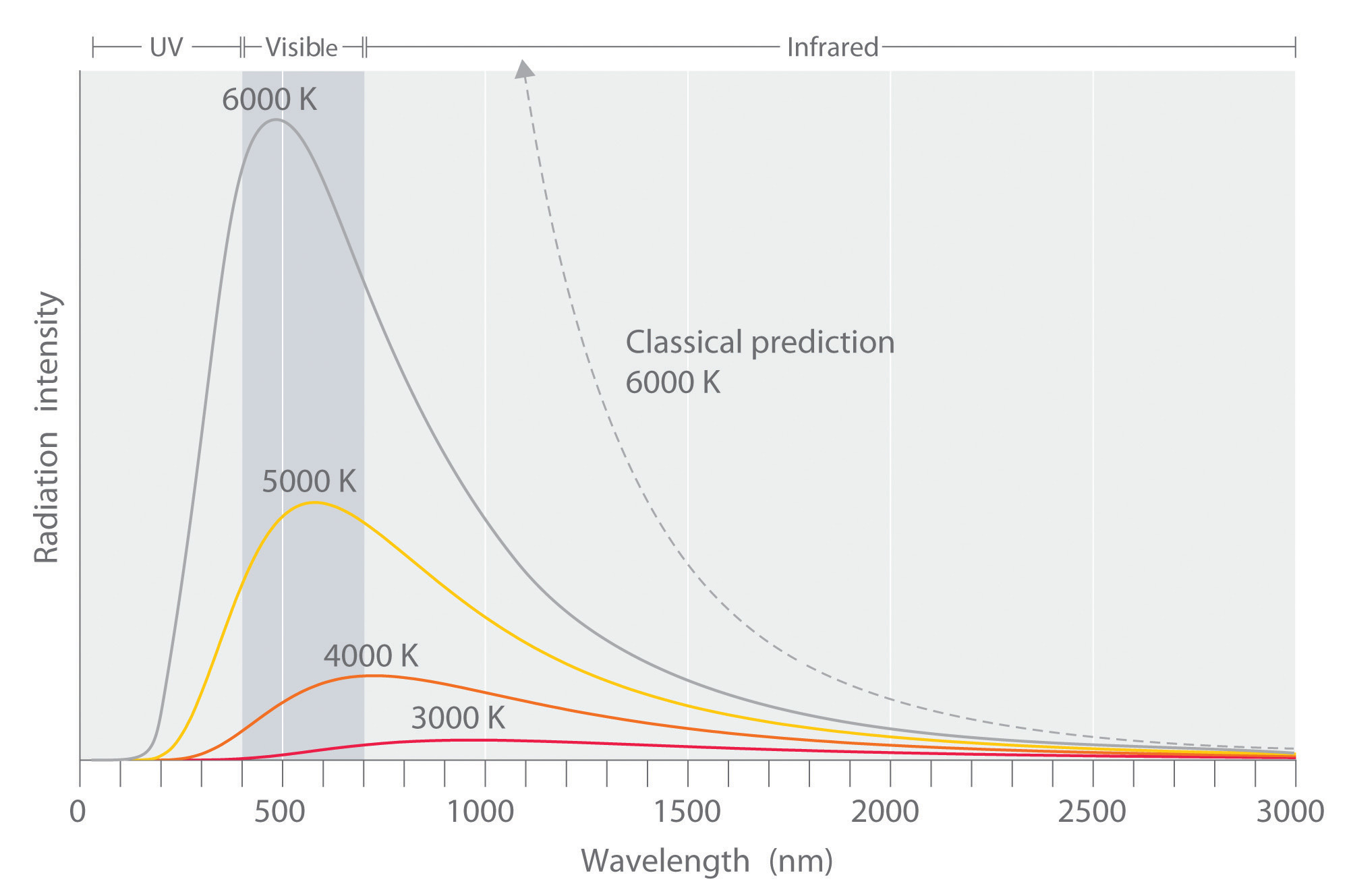
I dati sperimentali eseguiti sulla scatola nera hanno mostrato risultati leggermente diversi da quelli previsti dalla legge di Rayleigh-Jeans (Figura \(\PageIndex{5}). La legge era stata studiata e ampiamente accettata da molti fisici dell’epoca, ma i risultati sperimentali non mentivano, qualcosa era diverso tra ciò che era stato teorizzato e ciò che accade realmente. I risultati sperimentali mostravano una curva a campana, ma secondo la legge di Rayleigh-Jeans la frequenza divergeva man mano che ci si avvicinava alla regione ultravioletta (Equazione \ref{Eq3}\). Ehrenfest più tardi soprannominò questo fatto la “catastrofe ultravioletta”.
È importante sottolineare che l’equazione \(\ref{Eq3}\ è un risultato classico: gli unici input sono la dinamica classica e la teoria elettromagnetica di Maxwell. La carica \(e\) dell’oscillatore non appare: il risultato è indipendente dalla forza di accoppiamento tra l’oscillatore e la radiazione, l’accoppiamento deve solo essere abbastanza forte da garantire l’equilibrio termico. La derivazione della legge può essere trovata qui.
Rappresentazione differenziale vs. integrale della distribuzione
La radiazione è intesa come una distribuzione continua di ampiezza vs. lunghezza d’onda o, equivalentemente, vs. frequenza (Figura \(\PageIndex{5}). Ad una frequenza specifica \(\nu\), secondo la legge di Rayleigh-Jeans, la radiazione è
In pratica, è difficile misurare una singola frequenza e siamo più interessati agli intervalli di frequenza. Una frequenza esatta è il limite di una sequenza di intervalli sempre più piccoli. Se facciamo l’ipotesi che, per un intervallo sufficientemente piccolo, \(ρ(\nu,T)\) non varia, otteniamo la tua definizione per il differenziale \(dρ(ν,T)\) nell’equazione \ref{Eq3}:
L’ipotesi è giusta grazie alla continuità di \(ρ(\nu,T)\). Questa è l’approssimazione di un integrale su un intervallo molto piccolo \(d\nu\) per l’altezza di un punto all’interno di questo intervallo (\frac{8\pi k_bT\nu^2}{c^3}) per la sua lunghezza (\(d\nu\)). Quindi, se sommiamo una quantità infinita di piccoli intervalli come quello sopra, otteniamo un integrale. La radiazione totale tra \(\nu_1\) e \(\nu_2\) sarà:
Osserva che \(ρ(\nu,T)\ è quadratica in \(\nu\).
Esempio \(\PageIndex{4}\: la catastrofe ultravioletta
Qual è la radianza spettrale totale di un radiatore che segue la legge di Rayleigh-Jeans per il suo spettro di emissione?
Soluzione
La radianza spettrale totale \(\rho_{tot}(T)\) è l’emissione combinata su tutte le possibili lunghezze d’onda (o equivalentemente, frequenze), che è un integrale sulla relativa distribuzione (Equazione \ref{Eq3} per la legge di Rayleigh-Jeans).
&= \int_0^\infty \dfrac{8 \pi k_B T}{c^3} \nu^2 d\nu \end{align*}]
ma l’integrale
non converge. Peggio, è infinito,
Quindi, la legge di Rayleigh-Jeans di derivazione classica predice che la radianza di un corpo nero è infinita. Poiché la radianza è la potenza per angolo e unità di superficie, questo implica anche che la potenza totale e quindi l’energia che emette un corpo nero è infinita, il che è palesemente assurdo. Questa è chiamata la catastrofe ultravioletta perché la previsione assurda è causata dalla legge classica che non predice correttamente il comportamento alle alte frequenze/piccole lunghezze d’onda (Figura \(\PageIndex{5}).
Contribuenti
-
Michael Fowler (Beams Professor, Department of Physics, University of Virginia)
-
David M. Hanson, Erica Harvey, Robert Sweeney, Theresa Julia Zielinski (“Quantum States of Atoms and Molecules”)
-
Paul Flowers (University of North Carolina – Pembroke), Klaus Theopold (University of Delaware) e Richard Langley (Stephen F. Austin State University) con autori collaboratori. Il contenuto del libro di testo prodotto da OpenStax College è concesso in licenza Creative Commons Attribution License 4.0. Scarica gratuitamente su http://cnx.org/contents/85abf193-2bd…[email protected]).
- ACuriousMind (StackExchange)