Guinguette Marais Poitevin

Il metodo 3-4-5 per squadrare gli angoli

Di Robert Robillard su riparazioni e ristrutturazioni domestiche

3-4-5 Metodo Triangolo

La carpenteria non è una scienza esatta; è un approccio pragmatico per risolvere problemi, costruire e riparare. La mia esperienza mi ha insegnato che alcuni principi di base ci guidano su ciò che funzionerà o meno. Plumb, Level, and Square sono alcuni di questi principi.

3-4-5 Regola per assicurare layout quadrati

Carpentieri e costruttori spesso usano il metodo 3-4-5 per squadrare gli angoli e garantire che i progetti che stanno costruendo abbiano un preciso angolo di 90 gradi.

Nel mondo residenziale e delle costruzioni i falegnami spesso usano le squadre di velocità e le squadre di inquadramento per controllare i layout.

Quando il layout è grande queste squadre di inquadramento sono semplicemente troppo piccole per garantire la precisione necessaria. I grandi progetti di rimodellamento e costruzione, come la posa delle fondamenta di una casa o dei muri, spesso impiegano una tecnica di 3-4-5 triangoli per assicurare angoli accurati di 90 gradi.

Evitare gli errori di composizione

Non importa su quale progetto lavorate, se la vostra base o fondazione non è a livello, a piombo e quadrata, il resto del vostro progetto sarà fuori. Gli errori alla base di un ponte, di una casa o di un portico continueranno a crescere e ad aggravarsi nel momento in cui si arriva alle finiture, agli armadietti o si raggiunge l’intelaiatura del tetto.

3-4-5 Rule Layman’s Terms:

Se il lato corto del triangolo è 3 piedi, e la gamba che si estende da esso a 90 gradi è 4 piedi, l’ipotenusa, o gamba più lunga, sarà 5 piedi.

Questa tecnica richiede semplicemente che il carpentiere crei un triangolo nell’angolo delle linee che devono essere quadrate (90 gradi) tra loro.

Il triangolo 3-4-5 deve avere

• Un lato (gamba del triangolo) che è lungo 3 piedi
• Un secondo lato (gamba del triangolo) che è lungo 4 piedi
• Un terzo lato, che collega le due gambe che misura 5 piedi

Qualsiasi triangolo con lati di 3, 4, e 5 piedi avrà un angolo di 90 gradi di fronte al lato da 5 piedi. La bellezza e la semplicità di questa tecnica sono che se il carpentiere o il costruttore ha bisogno di aumentare la precisione su muri o strutture più grandi, qualsiasi multiplo della regola 3-4-5 può essere utilizzato.

Esempi della regola 3-4-5

• 3-4-5
• 6-8-10
• 9-12-15
• 12- 16-20
• 15-20-25

Perché funziona?

Matematicamente perché il metodo 3-4-5 per la squadratura degli angoli crea un angolo retto perfetto?

In geometria, un metodo ben noto per costruire l’angolo retto è quello di utilizzare il Teorema di Pitagora. Il matematico Pitagora scoprì una relazione tra i lati di qualsiasi triangolo rettangolo che ora è conosciuta come il Teorema di Pitagora. Pitagora dimostrò che il quadrato del lato più lungo (l’ipotenusa) è uguale alla somma dei quadrati degli altri due lati.

Questo è scritto come la seguente equazione:

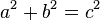
A e B sono le due gambe del triangolo rettangolo e C è l’ipotenusa. Se sostituiamo i numeri di un triangolo 3-4-5 in questa formula, abbiamo 9″ + 16″ = 25″

Ricordare il 3-4-5

Usare le dimensioni del triangolo di 3, 4 e 5 è facile da ricordare e da usare. Non ci sono equazioni difficili da ricordare e il metodo 3-4-5 produrrà sempre un perfetto angolo retto molto spesso.