La formula della velocità media è usata per trovare il tasso uniforme che comporta qualcosa che viaggia a un ritmo fisso e costante.
Per esempio, una macchina viaggia 3 ore. Percorre 30 miglia nella prima ora, 45 miglia nella seconda ora e 75 miglia nella terza ora.
Velocità nella prima ora = 30 miglia/ora
Velocità nella seconda ora = 45 miglia/ora
Velocità nella terza ora = 75 miglia/ora
Abbiamo tre velocità diverse nelle tre ore di viaggio.
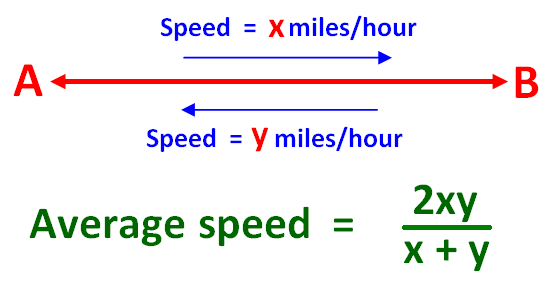
Se vogliamo trovare la velocità media per tutto il viaggio di tre ore, dobbiamo trovare il rapporto tra la distanza totale percorsa e il tempo totale impiegato.
Cioè, velocità costante = (30 + 45 + 75) / 3
= 150 / 3
= 50 miglia / ora
In base all’esempio precedente, la formula per trovare la velocità media è data qui sotto.
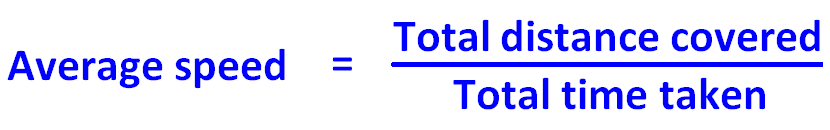
Se una persona viaggia da A a B ad una certa velocità, diciamo “x” miglia all’ora. Torna da B ad A ad una velocità diversa, diciamo “y” miglia all’ora. In entrambi i modi, copre la stessa distanza, ma a velocità diverse.
Allora, la formula per trovare la velocità media per l’intero viaggio è data qui sotto.
Formula della velocità media – Esempi
Esempio 1:
David ha guidato per 3 ore ad una velocità di 50 miglia all’ora, per 2 ore a 60 miglia all’ora e per 5 ore ad una velocità di 70 miglia all’ora. Qual è stata la sua velocità media per tutto il viaggio?
Risposta :
Step 1 :
La formula della velocità media è
= Distanza totale / Tempo totale impiegato.
E anche la formula per la distanza è
= Velocità ⋅ Tempo
Fase 2 :
La distanza percorsa nelle prime 3 ore è
= 50 ⋅ 3
= 150 miglia
La distanza percorsa nelle prossime 2 ore è
= 60 ⋅ 2
= 120 miglia
La distanza percorsa nelle ultime 5 ore è
= 70 ⋅ 5
= 350 miglia
Step 3 :
Allora, la distanza totale è
= 150 + 120 + 350
= 620 miglia
Il tempo totale è
= 3 + 2 + 5
= 10 ore
Step 4 :
Quindi, la velocità media è
= 620 / 10
= 62
Quindi, la velocità media per tutto il viaggio è di 62 miglia all’ora.
Esempio 2 :
Jose viaggia dal luogo A al luogo B ad una certa velocità. Quando torna dal luogo B al luogo A, la sua velocità è di 60 miglia all’ora. Se la velocità media per tutto il viaggio è di 72 miglia all’ora, trova la sua velocità quando viaggia dal luogo A a B.
Risposta :
Passo 1 :
Sia “a” la velocità dal luogo A a B.
Velocità dal luogo B ad A = 60 miglia/ora
Step 2 :
Qui, in entrambi i modi, copre la stessa distanza.
Allora, la formula per trovare la velocità media è
= 2xy / (x + y)
Step 3 :
x —-> Velocità dal luogo A a B
x = a
y —-> Velocità dal posto B ad A
y = 60
Passo 4 :
Dato: la velocità media è di 72 miglia/ora.
(2 ⋅ a ⋅ 60) / (a + 60) = 72
120a = 72(a + 60)
120a = 72a + 4320
48a = 4320
a = 90
Quindi, la velocità dal luogo A a B è di 90 miglia all’ora.
Esempio 3 :
David viaggia dal luogo A al luogo B ad una certa velocità. Quando torna dal luogo B al luogo A, aumenta la sua velocità di 2 volte. Se la velocità costante per tutto il viaggio è di 80 miglia all’ora, trova la sua velocità quando viaggia dal luogo A al luogo B.
Risposta :
Passo 1 :
Sia “a” la velocità dal luogo A a B.
Allora, la velocità dal posto B ad A = 2a
Passo 2 :
La distanza percorsa in entrambi i modi (A a B e B ad A) è la stessa.
Quindi, la formula per trovare la velocità media è
= 2xy / (x + y)
Step 3 :
x —-> Velocità dal luogo A a B
x = a
y —-> Velocità dal posto B ad A
y = 2a
Passo 4 :
Dato: Velocità media = 80 miglia/ora
(2 ⋅ a ⋅ 2a) / (a + 2a) = 80
4a² / 3a = 80
4a / 3 = 80
a = 60
Quindi, la velocità dal luogo A a B è di 60 miglia all’ora.
Esempio 4 :
Una persona impiega 5 ore per andare dal luogo A al luogo B alla velocità di 40 miglia all’ora. Torna dal luogo B al luogo A con una velocità aumentata del 25%. Trova la velocità media per l’intero viaggio.
Risposta :
Step 1 :
Velocità ( da A a B ) = 40 miglia/ora
Velocità ( da B ad A ) = 50 miglia/ora (25% aumentato)
Step 2 :
La distanza percorsa in entrambi i modi (da A a B e da B ad A) è la stessa.
Quindi, la formula per trovare la distanza media è
= 2xy / (x + y)
Step 3 :
x —-> Velocità dal luogo A a B
x = 40
y —-> Velocità dal posto B ad A
y = 50
Step 4 :
Velocità media = (2 ⋅ 40 ⋅ 50) / (40 + 50)
Velocità media = 44.44
Quindi, la velocità media per tutto il viaggio è di circa 44,44 miglia/ora.
Esempio 5 :
Velocità (da A a B) = 20 miglia/ora,
Velocità (da B a C) = 15 miglia/ora,
Velocità (da C a D ) = 30 miglia/ora
Se le distanze da A a B, da B a C e da C a D sono uguali e ci vogliono 3 ore per viaggiare da A a B, trova la velocità media da A a D.
Risposta :
Passo 1 :
La formula per trovare la distanza è
= Tasso ⋅ Tempo
Distanza da A a B è
= 20 ⋅ 3
= 60 miglia
Data : Le distanze da A a B, da B a C e da C a D sono uguali.
La distanza totale da A a D è
= 60 + 60 + 60
= 180 miglia
Step 2 :
La formula per trovare il tempo è
= Distanza / Velocità
Tempo (da A a B) = 60 / 20 = 3 ore
Tempo (da B a C) = 60 / 15 = 4 ore
Tempo (da C a D) = 60 / 30 = 2 ore
Il tempo totale impiegato da A a D è
= 3 + 4 + 2
= 9 ore
Step 3 :
La formula per trovare la velocità media è
= Distanza totale / Tempo totale tempo
= 180 / 9
= 20
Quindi, la velocità media da A a D è di 20 miglia all’ora.

Per avere più problemi sulla velocità media,
Si prega di cliccare qui
Oltre alle cose date sopra, se avete bisogno di altre cose, usate la nostra ricerca personalizzata di google qui.
Se hai qualche feedback sui nostri contenuti matematici, mandaci una mail:
Apprezziamo sempre il tuo feedback.
Potete anche visitare le seguenti pagine web su diversi argomenti di matematica.
PROBLEMI A PAROLA
Problemi a parola suHCF e LCM
Problemi a parola su equazioni semplici
Problemi a parola su equazioni lineari
Problemi a parola su equazioni quadratiche
Problemi di algebra
Problemi di parole sui treni
Problemi di parole su area e perimetro
Problemi di parole su variazione diretta e variazione inversa
Problemi di parole su prezzo unitario
Problemi di parole sul tasso unitario
Problemi di parole sul confronto dei tassi
Problemi di parole sulla conversione delle unità consuetudinarie
Problemi di parole sulla conversione delle unità metriche
Problemi di parole sul semplice interesse
Problemi di parole sull’interesse composto
Problemi di parole sui tipi di angoli
Problemi di parole sugli angoli complementari e supplementari
Problemi di parole sui fatti doppi
Problemi di trigonometria
Problemi di percentuali
Problemi di profitti e perdite
Problemi di segni e segni
Problemi di decimali
Problemi di frazioni
Problemi di parola su frazioni miste
Problemi di parola su equazioni a un passo
Problemi di parola su disuguaglianze lineari
Problemi di parola su rapporti e proporzioni
Problemi di parola su tempo e lavoro
Problemi di parola su insiemi e diagrammi di Venn
Problemi di parole sull’età
Problemi di parole sul teorema di Pitagora
Problemi di parole sulla percentuale di un numero
Problemi di parole sulla velocità costante
Problemi di parole sulla velocità media
Problemi di parole sulla somma degli angoli di un triangolo è 180 gradi
ALTRI ARGOMENTI
Profitti e perdite scorciatoie
Percentuali scorciatoie
Tempi della tabella dei tempi
Tempo, velocità e distanza
Scorciatoie per rapporti e proporzioni
Dominio e intervallo delle funzioni razionali
Dominio e intervallo delle funzioni razionali con buchi
Grafia delle funzioni razionali
Grafia di funzioni razionali con buchi
Conversione di decimali ripetuti in frazioni
Rappresentazione decimale di numeri razionali
Trovare la radice quadrata usando la divisione lunga
L.C.M per risolvere problemi di tempo e di lavoro
Tradurre i problemi di parole in espressioni algebriche
Rimontare quando 2 potenza 256 è divisa per 17
Rimontare quando 17 potenza 23 è divisa per 16
Somma di tutti i numeri a tre cifre divisibili per 6
Somma di tutti i numeri a tre cifre divisibili per 7
Somma di tutti i numeri a tre cifre divisibili per 8
Somma di tutti i numeri a tre cifre formati con 1, 3, 4
Somma di tutti e tre i numeri a quattro cifre formati con cifre non nulle
Somma di tutti e tre i numeri a quattro cifre formati con 0, 1, 2, 3
Somma di tutti e tre i numeri a quattro cifre formati con 1, 2, 5, 6