平均速度の計算式は、一定のペースで移動するものの均一な速度を求めるのに使われます。
例えば、ある車が3時間かけて移動します。
例えば、車が3時間かけて移動する場合、最初の1時間で30マイル、2時間目で45マイル、3時間目で75マイル移動します。
1時間目の速度 = 30マイル/時
2時間目の速度 = 45マイル/時
となります。
3時間目の速度 = 75マイル / 時
3時間の旅では3つの異なる速度があります。
3時間の旅全体の平均速度を求めるには、総走行距離と総走行時間の比を求めなければなりません。
つまり、次のようになります。 定速 = (30 + 45 + 75) / 3
= 150 / 3
= 50マイル/時
上の例をもとにします。 平均速度を求める計算式を以下に示します。
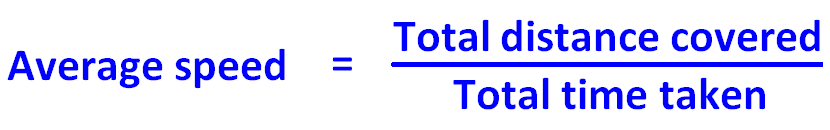
ある人がAからBまで、時速「x」マイルという速度で移動したとします。 また、BからAに戻る際には、時速「y」マイルという異なる速度で戻ってきます。 どちらの方法でも、距離は同じですが、速度は異なります。
そこで、全行程の平均速度を求めるための式を以下に示します。
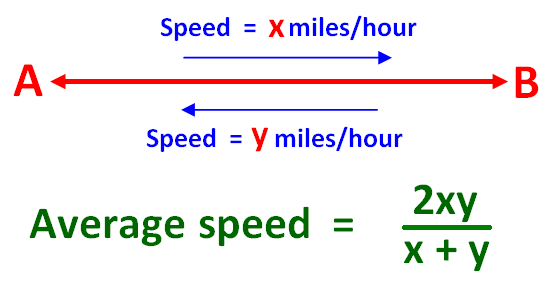
平均速度の公式 – 例
例1 :
Davidさんは、時速50マイルで3時間、時速60マイルで2時間、時速70マイルで5時間運転しました。
Answer :
Step 1 :
平均速度の公式は
= 総距離 / 総所要時間です。
また、距離の計算式は
= 率・時間
ステップ2 :
最初の3時間でカバーした距離は
= 50・3
です。
= 150マイル
次の2時間での走行距離は
= 60・2
= 120マイル
直近5時間の走行距離は
= 70 ÷ 5
= 350 マイル
ステップ3 :
すると。 合計距離は
= 150 + 120 + 350
= 620マイル
となります。
合計時間は
= 3 + 2 + 5
= 10時間
ステップ4 :
ですから、平均速度は
= 620 / 10
= 62
ですから、全行程の平均速度は時速62マイルです。
例2 :
ジョゼはある速さでA地点からB地点まで移動します。 全行程の平均速度を時速72マイルとすると、A地点からB地点に移動するときの速度を求めます。
答え :
Step 1 :
A地点からB地点までの速度を「a」とします。
B地点からA地点までの速度=時速60マイル
Step 2 :
ここでは、どちらの方法でも同じ距離をカバーしています。
すると、平均速度を求める式は
= 2xy / (x + y)
ステップ3 :
x —-> A地点からB地点までの速度
x = a
y -。—> B地点からA地点への速度
y = 60
ステップ4 :
Given : 平均速度は時速72マイルです。
(2・a・60) / (a + 60) = 72
120a = 72(a + 60)
120a = 72a + 4320
48a = 4320
a = 90
つまり。 の場合、A地点からB地点までの速度は時速90マイルです。
例3 :
デービッドさんは、ある速さでA地点からB地点まで移動します。 帰りは速度を2倍にして帰ってきました。 このときの定速を時速80マイルとすると、A地点からB地点に移動するときの速度を求めます。
答え :
ステップ1 :
A地点からB地点までの速度を「a」とします。
そうすると、B地点からA地点までの速度=2a
ステップ2 :
どちらの方法(A→B、B→A)でも移動距離は同じです。
従って、平均速度を求める式は
= 2xy / (x + y)
ステップ3 :
x —-> A地点からB地点までの速度
x = a
y -。—> B地点からA地点への速度
y = 2a
ステップ4 :
Given : 平均速度=時速80マイル
(2・a・2a) / (a + 2a) = 80
4a². / 3a = 80
4a / 3 = 80
a = 60
では、次のようになります。 A地点からB地点までの速度は時速60マイルです。
例4 :
ある人が時速40マイルでA地点からB地点まで5時間かけて移動しました。 その人はB地点からA地点へ25%増の速度で戻ってきました。 全行程の平均速度を求めなさい。
解答 :
ステップ1 :
速度(AからBへ)=時速40マイル
速度(BからAへ)=時速50マイル(25%アップ)
ステップ2 :
どちらの方法(AからB、BからA)でも移動距離は同じです。
従って、平均距離を求める式は
= 2xy / (x + y)
ステップ3 :
x —-> A地点からB地点までの速度
x = 40
y -。—> B地点からA地点への速度
y = 50
Step 4 :
平均速度 = (2・40・50) / (40 + 50)
平均速度 = 44.44
従って、全行程の平均速度は約44.44マイル/時です。
例5 :
速度(A→B)=時速20マイル、
速度(B→C)=時速15マイルです。
速度(C→D )=時速30マイル
AからB、BからC、CからDの距離が等しく、AからBまでの移動に3時間かかる場合、AからDまでの平均速度を求めます。
Answer :
Step 1 :
距離を求める式は
= 率・時間
AからBまでの距離は
となります。 AからBまでの距離は
= 20・3
= 60マイル
与えられた: AからB、BからC、CからDの距離は等しい。
AからDまでの総距離は
= 60 + 60 + 60
= 180マイル
ステップ2 :
時間を求める式は
= 距離 / 速度
です。
時間(A→B)=60 / 20 = 3時間
時間(B→C)= 60 / 15 = 4時間
時間(CからD)=60 / 30 = 2時間
AからDまでの総所要時間は AからDまでの所要時間は
= 3 + 4 + 2
= 9時間
ステップ3 :
平均速度を求める計算式は
= 総距離 / 総時間 時間
= 180 / 9
= 20
つまり、AからDまでの平均速度は AからDまでの平均速度は時速20マイルです。

平均速度に関する問題を増やすためです。
ここをクリックしてください
上記のものとは別に、他のものが必要な場合は、こちらのgoogleカスタム検索をご利用ください。
もし私たちの数学コンテンツについて何かご意見がありましたら、メールでご連絡ください:
私たちは常にあなたのフィードバックに感謝しています。
また、数学のさまざまな事柄について、以下のウェブページもご覧ください。
単語問題
HCFとLCMの単語問題
単純な方程式に関する単語問題
一次方程式に関する単語問題
二次方程式に関する単語問題
代数の言葉の問題
電車の言葉の問題
面積と外周の言葉の問題
直接変分と逆変分の言葉の問題
単価の言葉の問題
二次方程式の言葉の問題
p 単価
単価に関する言葉の問題
率の比較に関する言葉の問題
慣用単位の変換に関する言葉の問題
メートル単位の変換に関する言葉の問題
単 利息
複利に関する単語問題
角度の種類に関する単語問題
補角と補角の単語問題
二重の事実に関する単語問題
三角法の言葉の問題
パーセンテージの言葉の問題
利益と損失の言葉の問題
マークアップとマークダウンの言葉の問題
12進法の言葉の問題
分数の言葉の問題p
混合分数の言葉の問題
一段階の方程式の言葉の問題
線形不等式の言葉の問題
比率と割合の言葉の問題
時間と仕事の言葉の問題
集合とベン図の言葉の問題。
年齢に関する言葉の問題
ピタゴラスの定理に関する言葉の問題
数の割合に関する言葉の問題
一定の速度に関する言葉の問題
平均速度に関する言葉の問題
2.
三角形の角の和が180度であることに関する言葉の問題
その他のトピック
損益のショートカット
パーセンテージのショートカット
時刻表のショートカット
時間。 速度と距離のショートカット
比率と割合のショートカット
有理関数の領域と範囲
穴のある有理関数の領域と範囲
有理関数のグラフ作成p
穴のある有理関数のグラフ作成
繰り返しの小数を分数に変換する
有理数の10進法
長押しで平方根を求める
L.C.M法で時間や仕事の問題を解く
単語の問題を代数式に変換する
2の256乗を17で割ったときの余り
17の23乗を16で割ったときの余り。
6で割り切れる3桁の数字の総和
7で割り切れる3桁の数字の総和
8で割り切れる3桁の数字の総和
1, 3, 4で作られる3桁の数字の総和
1, 3, 4
0桁以外の4桁の数字の合計
0, 1, 2, 3
1, 2, 5, 6
1, 2, 5, 6を使った4桁の数字の合計。