「度数」は、数学ではいくつかの意味があります。
- 幾何学では角度を測る方法の1つである「度」
- しかし、ここでは代数学での「度」の意味を見てみましょう
代数学では「度」は「次数」と呼ばれることもあります
(変数が1つの)多項式の次数
多項式は次のようになります。
多項式の例
これは3項ある
(xのような1つの変数を持つ多項式の)次数は次の通りです。
More Examples:
| 4x | 次数は1( 指数を持たない変数は実際には1の指数を持つ) |
||
| 4×3 – x + 3 | 次数は3(xの最大の指数) | ||
| 4×3 – x + 3 | |||
| x2 + 2×5 – x | 次数は5(xの最大の指数) | ||
| z2 – z + 3 | 次数は2(zの最大指数) |
次数の名前
次数がわかったら、名前をつけることもできます!
| 学位 | 名前 | 例 |
|---|---|---|
| 0 | Constant | 7 |
| 1 | Linear | x+3 |
| 2 | Quadratic | x2-x+2 |
| 3 | Cubic | x3-x2+5 |
| 4 | 4次 元 | 6×4-x3+x-2 |
| 5 | 5進法 | x5-3×3+x2+8 |
例を挙げます。 y = 2x + 7は次数が1なので、一次方程式です
Example: 5w2 – 3は次数が2なので二次方程式です
高次方程式は通常、解くのが難しいです。
- 一次方程式は簡単に解けます
- 二次方程式は少し難しいです
- 二次方程式はまた難しいですが、助けとなる公式があります
- 四次方程式も解けますが、公式は非常に複雑です
- 五次方程式には公式がなく、解けないこともあります!
変数が2つ以上ある多項式の次数
変数が2つ以上ある多項式の場合、各項を見ていく必要があります。 項は+または-の記号で区切られています。
example of a polynomial
with more than one variable
For each term:
- その中の各変数の指数を足して次数を求め、
その中で最も大きい次数が多項式の次数です。
Example: What is the degree of this polynomial:
各項を確認します。
- 5xy2の次数は3(xの指数は1、yは2。
- 3x の次数は 1 (x の指数は 1)
- 5y3 の次数は 3 (y の指数は 3)
- 3 の次数は 0 (変数なし)
これらの中で最大の次数は 3 です (実際には 2 つの項が 3 の次数を持っています)。 したがって、この多項式の次数は3となります
例題です。 What is the degree of this polynomial:
4z3 + 5y2z2 + 2yz
各項を確認します。
- 4z3の次数は3(zの指数は3)
- 5y2z2の次数は4(yの指数は2、zの指数は2、2+2=4)
- 2yzの次数は2(yの指数は1、zの指数は1, そして1+1=2)
これらのうち最大の次数は4なので、この多項式の次数は4です
書き出し
「(何であれ)の次数は3」と言う代わりに、次のように書きます。
![]()
式が分数の場合
有理式(分数の形をしているもの)の次数は、上(分子)の次数を取り、下(分母)の次数を引くことで求めることができます。
以下に3つの例を示します。
Calculating Other Types of Expressions
Warning:
私たちは時々、…
- 関数の対数を
- 変数の対数で割ることによって、式の次数を計算することができます
…そして、答えが「どこに向かっているか」を見るために、より大きな値に対してそれを行います。
(より正確にはln(f(x))/ln(x)のLimit to Infinityを計算するべきですが、ここではシンプルにしたいと思います)
|
注:”ln “は自然対数関数です。 |
 |
ここに例があります:
Example: (3+xの平方根)の次数は何ですか?
xの値を大きくしてみましょう。
| x | ln( |
ln(x) | ln( / ln(x) |
||
|---|---|---|---|---|---|
| 2 | 1.48483 | 0.69315 | 2.1422 | ||
| 4 | 1.60944 | 1.60944 | 1.38629 | 1.38629 | 1.1610 |
| 10 | 1.81845 | 2.30259 | 0.7897 | ||
| 100 | 2.56495 | 4.60517 | 0.5570 | ||
| 1,000 | 3.54451 | 6.90776 | 0.5131 | ||
| 10,000 | 4.63473 | 9.21034 | 0.5032 | ||
| 100,000 | 5.76590 | 11.51293 | 0.5008 | ||
| 1,000,000 | 6.91075 | 13.81551 | 0.5002 |
表を見てみると
- xが大きくなるとln(
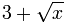 ) / ln(x)はどんどん0.5に近づいていきます
) / ln(x)はどんどん0.5に近づいていきます
つまり、度数は0.5(言い換えれば1/2)
(注: これは x½ = x の平方根とうまく一致します。
Some Degree Values
| Expression | Degree |
|---|---|
| log(x) | 0 |
| ex | ∞ |
| 1/x | -1 |
| 1/2 |
となります。



