Guinguette Marais Poitevin

The 3-4-5 Method For Squaring Corners

By Robert Robillard on Home Repairs and Remodeling

3-4-5 Triangle Method

大工仕事は正確な科学ではなく、問題解決、建築、修理に対する実際的なアプローチです。 私の経験から、いくつかの基本的な原則が、何がうまくいくのか、あるいはうまくいかないのかを教えてくれました。

3-4-5 Rule To Ensure Square Layouts

大工や建築家は、3-4-5法を使ってコーナーを四角くし、作っているプロジェクトが正確に90度の角度を持っていることを確認します。

住宅や建築の世界では、大工さんはレイアウトをチェックするためにスピードスクエアやフレーミングスクエアをよく使います。

レイアウトが大きい場合、これらのフレーミングスクエアでは小さすぎて必要な精度を保証できません。

Avoid Compounding Errors

どのようなプロジェクトであっても、土台や基礎が水平でなく、垂直でなく、四角でなければ、プロジェクトの残りの部分がずれてしまいます。 デッキや家、ポーチの基礎部分でのエラーは、仕上げのトリムやキャビネット、屋根の骨組みにたどり着くまでにどんどん大きくなり、複合的になっていきます。

3-4-5 Rule Layman’s Terms:

三角形の短辺が3フィート、そこから90度に伸びる脚が4フィートの場合、斜辺、つまり最も長い脚は5フィートになります。

このテクニックは、単純に、大工さんが、互いに直角(90度)になるような線の角に三角形を作ることを要求しています。

3-4-5の三角形は、

• 1つの辺(三角形の脚)の長さが3フィート
• 2つ目の辺(三角形の脚)の長さが4フィート
• 2つの脚をつなぐ3つ目の辺の長さが5フィート

3、4、5フィートの辺を持つ三角形は、5フィートの辺と90度の角度を持つことになります。 このテクニックの美しさとシンプルさは、大工やビルダーがより大きな壁や構造物の精度を上げる必要がある場合、3-4-5 ルールの任意の倍数を展開できることです。

3-4-5ルールの例

• 3-4-5
• 6-8-10
• 9-12-15
• 12-16-20
• 15-20-25

なぜこのテクニックが有効なのか？

数学的に、角を四角くする 3-4-5 の方法が完全な直角を作るのはなぜでしょうか?

幾何学では、直角を作るためのよく知られた方法として、ピタゴラスの定理を採用しています。 数学者のピタゴラスが発見した直角三角形の辺の関係は、現在では「ピタゴラスの定理」として知られています。

これは次の式で表されます。

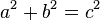
AとBは直角三角形の2本の脚で、Cは斜辺です。 この式に3-4-5の三角形の数字を代入すると、9″＋16″＝25″となります

Remembering the 3-4-5

三角形の寸法を3、4、5とするのは覚えやすく、展開しやすいです。