この質問は思っているよりも複雑です

地球を持ち上げるのに必要なアリの数は? これはとても簡単な質問のように思えるかもしれません。 基本的には、2つのことを知る必要があります。 1つは、1匹のアリが持ち上げられる質量、もう1つは、地球の質量です。 2つ目の数字を1つ目の数字で割れば、目的の答えが得られます。
さて、まず最初に、この小さな思考実験では、どこで地球を持ち上げるかを決める必要があります。 通常、「Yを持ち上げるのにどれだけのXが必要か」という質問をするときは、「地球上で」という意味です。 そのためには、地球上で地球を持ち上げなければなりませんが、これは思考実験なので、それは気にしないことにしましょう。 私たちは地球上にいて、アリに持ち上げてもらいたい「第2の地球」E2があるとします。
E2には、地球と同じ重力場があります。
さて、先ほど言ったように、E2の質量を1匹のアリが持ち上げられる質量で割ればいいんですよね? そうではありません。 この問題は、もう少し複雑です。 この方法は、本や石、あるいはバスのような「普通」の物体には有効です。 しかし、E2はこれよりもはるかに重いのです。 そのため、地球と同じ重力場を持っています(質量が地球と同じなので)。 通常の物体の落下では、地球の重力場だけを考慮すればよく、物体の重力場は事実上存在しません。 このような場合、地球が物体に与える力は、物体の質量(キログラム)に9.81を乗じてニュートン単位の力とすれば、簡単に計算できます。
私たちが知る必要があるのは、仮想のE2を地球に対して維持する力です。
私たちが知る必要があるのは、仮想のE2を地球に対して維持する力です。 そして、この力を打ち消すのに必要なアリの数を計算することができます。 E2 を抑える力は、次の式で計算できます。距離 r のある 2 つの質量 (両方とも m で示される) の間の力 F を計算します。
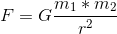
Gは重力定数です。 E2が地球上に「座って」いる場合、両方の質量の中心は12742000メートル(地球の半径の2倍)離れています。 数式の残りの数字を埋めると、1.4662378 * 10²⁵ニュートンの力が得られます。 興味深いことに、この数値は、地球に向かって落下する「通常の」物体の場合と同じように力を計算した場合(9.81倍)に比べて、数倍も小さくなっています。 ゲーム内に独自の力を持つ重力体があるにもかかわらず、結果として力が小さくなっているのです。 なぜそんなことが可能なのでしょうか? その答えは「距離」です。 地球から離れれば離れるほど、重力は小さくなり、E2の中心は地球の表面から6371キロメートル離れています。
人間1人を運ぶのに十分なアリがいます。 アリがどれだけの力を発揮できるのかを知る必要があります。 蟻がどれくらい持ち上げられるかについては、様々な数字が出ていますが、私は自分の体重の50倍という数字を使うことにします。 これに、アリの体重が例えば2ミリグラムだとします。 体重の50倍は100ミリグラムとなり、持ち上げられる力は0.000981ニュートンとなります。 1.4662378 * 10²⁵ニュートンが必要なので、約1.49 * 10²⁸匹のアリが必要になります。 現在、地球上のアリの総量は10⁶と推定されているので、地球を持ち上げるにはアリの数が足りません。 しかし、興味深いことに、私たちは全人類を運ぶのに十分な数を持っています。 10⁶匹のアリと7.73 * 10⁹人の人間では、人間1人に対して100万匹以上のアリがいることになります。 1匹2ミリグラムのアリが100万匹いると、総質量は2kgになります。 体積の50倍の重さを運べるとすると、100kgになります。 平均的な人間はこれよりずっと軽いのです!