Guinguette Marais Poitevin

De 3-4-5 Methode Voor Het Squaren Van Hoeken

Door Robert Robillard op Home Repairs And Remodeling

3-4-5 Driehoek Methode

Schrijnwerk is geen exacte wetenschap; het is een pragmatische benadering van het oplossen van problemen, bouwen, en repareren. Mijn ervaring heeft me geleerd dat een paar basisprincipes ons leiden over wat wel en wat niet zal werken. Loodrecht, waterpas en haaks is een aantal van die principes.

3-4-5 Regel Om Vierkante Layouts te Verzekeren

Timmerlieden en bouwers gebruiken vaak de 3-4-5 methode voor het haaks maken van hoeken en zorgen ervoor dat de projecten die zij bouwen een precieze hoek van 90 graden hebben.

In de woning- en bouwwereld gebruiken timmerlieden vaak speed squares en framing squares om lay-outs te controleren.

Wanneer de lay-out groot is, zijn deze framing squares gewoon te klein om de benodigde nauwkeurigheid te garanderen. Bij grote verbouwings- en bouwprojecten, zoals het leggen van de fundering van een huis of muren, wordt vaak gebruik gemaakt van een 3-4-5 driehoekstechniek om nauwkeurige hoeken van 90 graden te garanderen.

Vermijd opeenstapelende fouten

Hoe je ook werkt, als de fundering niet waterpas, loodrecht en haaks is, zal de rest van je project niet goed zijn. Fouten aan de basis van een terras, huis of veranda zullen blijven groeien en zich uitbreiden tegen de tijd dat u de afwerking, kasten, of het dak framing bereikt.

3-4-5 regel lekentaal:

Als de korte zijde van de driehoek 3 voet is, en het been dat 90 graden uitsteekt 4 voet, dan is de hypotenusa, of langste been, 5 voet.

Deze techniek vereist simpelweg dat de timmerman een driehoek maakt in de hoek van de lijnen die haaks (90 graden) op elkaar moeten staan.

De 3-4-5 driehoek moet

• Een zijde (driehoeksbeen) die 3 voet lang is
• Een tweede zijde (driehoeksbeen) die 4 voet lang is
• Een derde zijde, die de twee benen verbindt en 5 voet lang is

Elke driehoek met zijden van 3, 4, en 5 voet zal een hoek van 90 graden hebben tegenover de zijde van 5 voet. Het mooie en eenvoudige van deze techniek is dat als de timmerman of bouwer de nauwkeurigheid van grotere muren of constructies wil vergroten, elk veelvoud van de 3-4-5 regel kan worden toegepast.

Voorbeelden van de 3-4-5 regel

• 3-4-5
• 6-8-10
• 9-12-15
• 12- 16-20
• 15-20-25

Waarom werkt dit?

Waarom levert de 3-4-5 methode voor het kwadrateren van hoeken een perfecte rechte hoek op?

In de meetkunde is een bekende methode om de rechte hoek te construeren het gebruik van de Stelling van Pythagoras. De wiskundige Pythagoras ontdekte een verband tussen de zijden van een willekeurige rechthoekige driehoek, dat nu bekend staat als de Stelling van Pythagoras. Pythagoras bewees dat het kwadraat van de langste zijde (de schuine zijde) gelijk is aan de som van de kwadraten van de overige twee zijden.

Dit wordt geschreven als de volgende vergelijking:

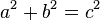
A en B zijn de twee benen van de rechthoekige driehoek en C is de schuine zijde. Als we de getallen van een 3-4-5 driehoek in deze formule substitueren, krijgen we 9″ + 16″ = 25″

De 3-4-5 onthouden

Het gebruik van driehoeksafmetingen van 3, 4, en 5 is gemakkelijk te onthouden en in te zetten. Er zijn geen moeilijke vergelijkingen om te onthouden en de 3-4-5 methode zal altijd een perfecte rechte hoek opleveren.