Guinguette Marais Poitevin

Obliczenia PPT wykonuje się w zakresie E, co oznacza, że pole lasera jest traktowane jako fale elektromagnetyczne. Szybkość jonizacji może być również obliczana w A-gauge, który podkreśla cząsteczkową naturę światła (pochłanianie wielu fotonów podczas jonizacji). Takie podejście zostało przyjęte przez model Krainova oparty na wcześniejszych pracach Faisala i Reissa. Otrzymana w ten sposób szybkość jest dana przez

W K R A = ∑ n = N ∞ 2 π ω 2 p ( n – n o s c ) 2 ∫ d Ω | F T ( I K A R Ψ ( r ) | 2 J n 2 ( n f , n o s c 2 ) { {displaystyle W_{KRA}= ^sum _{n=N}^{infty }2\pi \omega ^{2}p \left(n-n_{mathrm {osc} } }prawo)^{2}int \mathrm {d} \^{2}J_{n}^{2}}pp(n_{f},^{frac {n_{mathrm {osc} }}{2}}}prawda)}

gdzie:

• n i = E i / ω , {{displaystyle n_{i}=E_{i}/ /omega ,}
  

• n o s c = U p / ω {{displaystyle n_{mathrm {osc} }=U_{p}/omega }
  

  z U p {{displaystyle U_{p}}.

  

  jest energią ponderomotoryczną,

• N = {{displaystyle N=}
  

  jest minimalną liczbą fotonów potrzebną do zjonizowania atomu,

• J n ( u , v ) {{displaystyle J_{n}(u,v)}
  

  jest podwójną funkcją Bessela,

• p = 2 ω ( n – n o s c – n i ) , {{displaystyle p={sqrt {2omega (n-n_{mathrm {osc} } }-n_{i})}}}
  

• n f = 2 n o s c / ω p cos ( θ ) {{displaystyle n_{f}=2{sqrt {n_{mathrm {osc} }/omega }}p cos(™theta )}
  

  z θ {displaystyle itha }

  

  kąt pomiędzy momentem pędu elektronu, p, a polem elektrycznym lasera, F,

• FT jest trójwymiarową transformatą Fouriera, oraz

• I K A R = ( 2 Z 2 n 2 F r ) n {displaystyle I_{KAR}=left({frac {2Z^{2}}{n^{2}Fr}}}right)^{n}}.
  

  uwzględnia poprawkę Coulomba w modelu SFA.

Stabilizacja atomu/pułapka populacjiEdit

W obliczaniu szybkości MPI atomów rozważane są tylko przejścia do stanów kontinuum. Takie przybliżenie jest akceptowalne tak długo, jak długo nie występuje rezonans wielofotonowy pomiędzy stanem podstawowym a niektórymi stanami wzbudzonymi. Jednak w rzeczywistej sytuacji oddziaływania z laserami impulsowymi, podczas ewolucji natężenia lasera, ze względu na różne przesunięcia Starka stanu podstawowego i wzbudzonego istnieje możliwość, że niektóre stany wzbudzone wejdą w rezonans wielofotonowy ze stanem podstawowym. W ramach obrazu atomu ubranego, stan podstawowy ubrany przez m {{displaystyle m}}

fotonów, a stan rezonansowy ulega unikniętemu przejściu przy intensywności rezonansu I r {{displaystyle I_{r}}

. Minimalna odległość, V m {displaystyle V_{m}}

, przy unikniętym przejściu jest proporcjonalna do uogólnionej częstotliwości Rabiego, Γ ( t ) = Γ m I ( t ) m / 2 {displaystyle Γ m I ( t ) m / 2 {displaystyle Γ m I ( t ) m / 2}

sprzężenie dwóch stanów. Według Story’ego i in. prawdopodobieństwo pozostania w stanie podstawowym, P g {{displaystyle P_{g}}

, jest dane przez P g = exp ( – 2 π W m 2 d W / d t ) {displaystyle P_{g}}=exp left(-{frac {2}pi W_{m}^{2}}{{mathrm {d} W/{mathrm {d} t}}}right)}

gdzie W {{displaystyle W}

jest zależną od czasu różnicą energii pomiędzy dwoma ubranymi stanami. W oddziaływaniu z krótkim impulsem, jeżeli rezonans dynamiczny jest osiągany we wznoszącej lub opadającej części impulsu, populacja praktycznie pozostaje w stanie podstawowym i efekt rezonansów wielofotonowych może być zaniedbany. Jeśli jednak stany wejdą w rezonans w szczycie impulsu, gdzie d W / d t = 0 {{displaystyle \mathrm {d} W / d t = 0 {displaystyle \mathrm {d}

, to stan wzbudzony jest zasiedlony. Po zasiedleniu, ponieważ potencjał jonizacji stanu wzbudzonego jest mały, można się spodziewać, że elektron zostanie natychmiast zjonizowany.

W 1992 r. de Boer i Muller pokazali, że atomy Xe poddane krótkim impulsom laserowym mogą przetrwać w silnie wzbudzonych stanach 4f, 5f i 6f . Uważano, że stany te zostały wzbudzone przez dynamiczne przesunięcie Starka poziomów do rezonansu wielofotonowego z polem podczas wznoszącej części impulsu laserowego. Dalsza ewolucja impulsu laserowego nie zjonizowała całkowicie tych stanów pozostawiając pewne wysoko wzbudzone atomy. Zjawisko to będziemy nazywać „pułapkowaniem populacji”.

Schematyczne przedstawienie pułapkowania populacji typu lambda. G jest stanem podstawowym atomu. 1 i 2 to dwa zdegenerowane stany wzbudzone. Po przeniesieniu populacji do tych stanów w wyniku rezonansu wielofotonowego, stany te są sprzężone poprzez continuum c i populacja zostaje uwięziona w superpozycji tych stanów.

Przywołujemy obliczenia teoretyczne, że niepełna jonizacja występuje zawsze, gdy występuje równoległe wzbudzenie rezonansowe do wspólnego poziomu ze stratą jonizacji. Rozważamy stan taki jak 6f z Xe, który składa się z 7 poziomów quasi-degeneratywnych w zakresie szerokości pasma lasera. Poziomy te wraz z kontinuum tworzą układ lambda. Mechanizm pułapkowania typu lambda jest schematycznie przedstawiony na rysunku. W początkowej części impulsu (a) stan wzbudzony (z dwoma zdegenerowanymi poziomami 1 i 2) nie jest w rezonansie multifotonowym ze stanem podstawowym. Elektron jest zjonizowany poprzez sprzężenie wielofotonowe z kontinuum. Wraz ze wzrostem natężenia impulsu stan wzbudzony i kontinuum ulegają przesunięciu energetycznemu na skutek przesunięcia Starka. W szczytowym momencie impulsu (b) stany wzbudzone wchodzą w rezonans wielofotonowy ze stanem podstawowym. Gdy natężenie zaczyna maleć (c), oba stany są sprzężone poprzez kontinuum i populacja zostaje uwięziona w koherentnej superpozycji obu stanów. Przy kolejnym działaniu tego samego impulsu, z powodu interferencji w amplitudach przejść układu lambda, pole nie jest w stanie całkowicie zjonizować populacji i część populacji zostanie uwięziona w koherentnej superpozycji quasi zdegenerowanych poziomów. Zgodnie z tym wyjaśnieniem stany o większym momencie pędu – z większą ilością podpoziomów – miałyby większe prawdopodobieństwo uwięzienia populacji. W ogólności siła pułapkowania będzie zdeterminowana przez siłę sprzężenia dwóch fotonów pomiędzy quasi-zdegenerowanymi poziomami poprzez kontinuum. W 1996 roku, używając bardzo stabilnego lasera i minimalizując efekty maskowania wynikające z rozszerzania się obszaru ogniskowego wraz ze wzrostem intensywności, Talebpour et al. zaobserwowali struktury na krzywych pojedynczo naładowanych jonów Xe, Kr i Ar. Struktury te zostały przypisane pułapkowaniu elektronów w silnym polu lasera. Bardziej jednoznaczna demonstracja pułapkowania populacji została przedstawiona przez T. Morishitę i C. D. Lin.

Niesekwencyjna wielokrotna jonizacjaEdit

Zjawisko niesekwencyjnej jonizacji (NSI) atomów wystawionych na działanie intensywnych pól laserowych jest przedmiotem wielu teoretycznych i eksperymentalnych badań od 1983 roku. Pionierskie prace rozpoczęły się od obserwacji struktury „kolana” na krzywej sygnału jonów Xe2+ w funkcji intensywności przez L’Huillier et al. Z eksperymentalnego punktu widzenia, podwójna jonizacja NS odnosi się do procesów, które w jakiś sposób zwiększają szybkość produkcji podwójnie naładowanych jonów o ogromny czynnik przy intensywnościach poniżej intensywności nasycenia pojedynczo naładowanych jonów. Z drugiej strony, wielu z nich woli definiować NSI jako proces, w którym dwa elektrony są jonizowane prawie jednocześnie. Definicja ta implikuje, że poza kanałem sekwencyjnym A + L – > A + + L – > A + + { {{}}} A+L->A^{+}+L->A^{++}}

istnieje jeszcze jeden kanał A + L – > A + + {{}} A+L->A^{++}}

co stanowi główny wkład w produkcję podwójnie naładowanych jonów przy niższych intensywnościach. Pierwszą obserwację potrójnego NSI w argonie oddziałującym z laserem o długości fali 1 µm opisali Augst i in. Później, badając systematycznie NSI wszystkich atomów gazów rzadkich, zaobserwowano poczwórne NSI Xe. Najważniejszym wnioskiem z tych badań było zaobserwowanie następującej zależności pomiędzy szybkością NSI do dowolnego stanu naładowania a szybkością jonizacji tunelowej (przewidywanej wzorem ADK) do poprzednich stanów naładowania; W N S ( A n + ) = ∑ i = 1 n – 1 α n ( λ ) W A D K ( A i + ) { {displaystyle W_{NS}(A^{n+})=suma _{i=1}^{n-1} ∑ W_{ADK} ∑left(∑lambda ∑right)}

gdzie W A D K ( A i + ) {displaystyle W_{ADK}}}left(A^{i+}}}

jest szybkością quasi-statycznego tunelowania do i’ego stanu naładowania, a α n ( λ ) {{displaystyle \a_{n}(\a_lambda )}

są pewnymi stałymi zależnymi od długości fali lasera (ale nie od czasu trwania impulsu).

Dwa modele zostały zaproponowane do wyjaśnienia niesekwencyjnej jonizacji; model shake-off i model ponownego rozpraszania elektronów. Model shake-off (SO), zaproponowany po raz pierwszy przez Fittinghoffa et al., został zaadoptowany z dziedziny jonizacji atomów przez promienie X i pociski elektronowe, gdzie proces SO jest jednym z głównych mechanizmów odpowiedzialnych za wielokrotną jonizację atomów. Model SO opisuje proces NS jako mechanizm, w którym jeden elektron zostaje zjonizowany przez pole laserowe, a odejście tego elektronu jest tak gwałtowne, że pozostałe elektrony nie mają wystarczająco dużo czasu na dostosowanie się do nowych stanów energetycznych. Istnieje więc pewne prawdopodobieństwo, że po jonizacji pierwszego elektronu, drugi elektron zostanie wzbudzony do stanów o wyższej energii (shake-up) lub nawet zjonizowany (shake-off). Należy zaznaczyć, że do tej pory nie przeprowadzono ilościowych obliczeń w oparciu o model SO, a model ten ma nadal charakter jakościowy.

Model rozpraszania elektronów został opracowany niezależnie przez Kuchiewa, Schafera i innych, Corkuma, Beckera i Faisala oraz Faisala i Beckera. Główne cechy tego modelu można łatwo zrozumieć z wersji Corkuma. Model Corkuma opisuje jonizację NS jako proces, w którym elektron jest zjonizowany tunelowo. Elektron ten następnie oddziałuje z polem laserowym, gdzie jest przyspieszany z dala od jądra atomowego. Jeśli elektron został zjonizowany w odpowiedniej fazie pola, to pół cyklu później przejdzie obok pozycji pozostałego jonu, gdzie może uwolnić dodatkowy elektron poprzez zderzenie elektronowe. Tylko przez połowę czasu elektron jest uwalniany w odpowiedniej fazie, a przez drugą połowę nigdy nie wraca do jądra atomowego. Maksymalna energia kinetyczna, jaką może mieć powracający elektron, jest 3,17 razy większa od potencjału ponderomotorycznego ( U p {{p}}).

) lasera. Model Corkuma nakłada granicę odcięcia na minimalne natężenie ( U p {displaystyle U_{p}}

jest proporcjonalne do natężenia), gdzie może wystąpić jonizacja spowodowana ponownym rozpraszaniem.

Diagram Feynmana dla procesu podwójnej jonizacji w atomie poprzez mechanizm ponownego rozpraszania

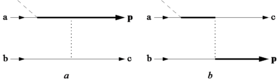
Model ponownego rozpraszania w wersji Kucziewa (model Kucziewa) jest modelem kwantowo-mechanicznym. Podstawowa idea tego modelu jest zilustrowana diagramami Feynmana na rysunku a. Najpierw oba elektrony znajdują się w stanie podstawowym atomu. Linie oznaczone a i b opisuj± odpowiadaj±ce im stany atomu. Następnie elektron a zostaje zjonizowany. Pocz±tek procesu jonizacji jest pokazany przez przecięcie z pochył± lini± przerywan±. gdzie zachodzi MPI. Propagacja zjonizowanego elektronu w polu lasera, podczas której absorbuje on inne fotony (ATI), jest pokazana pełną grubą linią. Zderzenie tego elektronu z macierzystym jonem atomowym jest pokazane pionową przerywaną linią reprezentującą oddziaływanie Coulomba pomiędzy elektronami. Stan oznaczony przez c opisuje wzbudzenie jonu do stanu dyskretnego lub continuum. Rysunek b opisuje proces wymiany. Model Kucziewa, w przeciwieństwie do modelu Corkuma, nie przewiduje żadnego progowego natężenia dla wystąpienia jonizacji NS.

Kucziew nie uwzględnił efektów Coulomba na dynamikę zjonizowanego elektronu. Spowodowało to ogromne niedoszacowanie szybkości podwójnej jonizacji. Oczywiście, w podejściu Beckera i Faisala (które jest w duchu równoważne modelowi Kucziewa), ta wada nie istnieje. W rzeczywistości, ich model jest dokładniejszy i nie cierpi na dużą liczbę przybliżeń dokonanych przez Kucziewa. Wyniki ich obliczeń doskonale pasuj± do wyników eksperymentalnych Walkera et al. Becker i Faisal byli w stanie dopasować wyniki eksperymentalne dla wielokrotnych NSI atomów gazów rzadkich za pomoc± swojego modelu. W rezultacie, ponowne rozpraszanie elektronów może być przyjęte jako główny mechanizm występowania procesu NSI.

Wielokrotna jonizacja elektronów walencyjnych i fragmentacja cząsteczek poliomerów

Jonizacja wewnętrznych elektronów walencyjnych jest odpowiedzialna za fragmentację cząsteczek poliomerów w silnych polach laserowych. Zgodnie z modelem jakościowym dysocjacja molekuł zachodzi poprzez trzystopniowy mechanizm:

• MPI elektronów z wewnętrznych orbitali molekuły, w wyniku czego powstaje jon molekularny na poziomach ro-wibracyjnych wzbudzonego stanu elektronowego;
• Szybkie bezpromieniste przejście na wysoko leżące poziomy ro-wibracyjne niższego stanu elektronowego; oraz
• Substancjalna dysocjacja jonu na różne fragmenty poprzez różne kanały fragmentacyjne.

.