Co to jest prawdopodobieństwo łączne?
Prawdopodobieństwo łączne jest rodzajem miary znalezionej poprzez obliczenie prawdopodobieństwa wystąpienia dwóch zdarzeń razem. Innymi słowy, jest to prawdopodobieństwo zdarzenia X zachodzącego w tym samym czasie co zdarzenie Y, jak przecięcie dwóch zdarzeń.
Prawdopodobieństwo łączne dla zdarzeń zależnych
Aby zmierzyć prawdopodobieństwo łączne, oba zdarzenia muszą wystąpić w tym samym czasie i muszą być od siebie niezależne. Oznacza to, że wspólne prawdopodobieństwo dla zdarzeń zależnych nie może być określone.
Powiedzmy, że chcesz określić czy będzie padać w tym samym czasie, kiedy na niebie będą chmury. Te dwa zdarzenia są zależne od siebie, ponieważ kiedy pada deszcz, najprawdopodobniej będą występować chmury. Dlatego te zdarzenia są od siebie zależne.
Zamiast wspólnego prawdopodobieństwa, do zdarzeń zależnych należy używać prawdopodobieństwa warunkowego.
Prawdopodobieństwo łączne dla zdarzeń niezależnych
Jak wspomniano, aby określić prawdopodobieństwo łączne, oba zdarzenia muszą być niezależne od siebie. Na przykład, prawdopodobieństwo otrzymania „reszki” lub „główki” w rzucie monetą są niezależnymi zdarzeniami. Innymi słowy, prawdopodobieństwo otrzymania reszki w pierwszym rzucie nie będzie miało wpływu na prawdopodobieństwo otrzymania główki, gdy rzucisz monetą po raz drugi.
Jak obliczyć prawdopodobieństwo łączne
Podczas nauki jak obliczyć prawdopodobieństwo łączne, ważne jest aby zrozumieć, że wzór wymaga aby dwa zdarzenia były niezależne od siebie. Oznacza to, że wynik jednego zdarzenia nie może wpływać na wpływ wyniku drugiego zdarzenia. Przed obliczeniem wspólnego prawdopodobieństwa należy zadać sobie pytanie, czy wynik jednego zdarzenia będzie miał wpływ na wynik drugiego.
Ponieważ wspólne prawdopodobieństwo można opisać jako „przecięcie dwóch zdarzeń”, wzór będzie zawierał te dwa zdarzenia – i jak mogą się one przecinać.
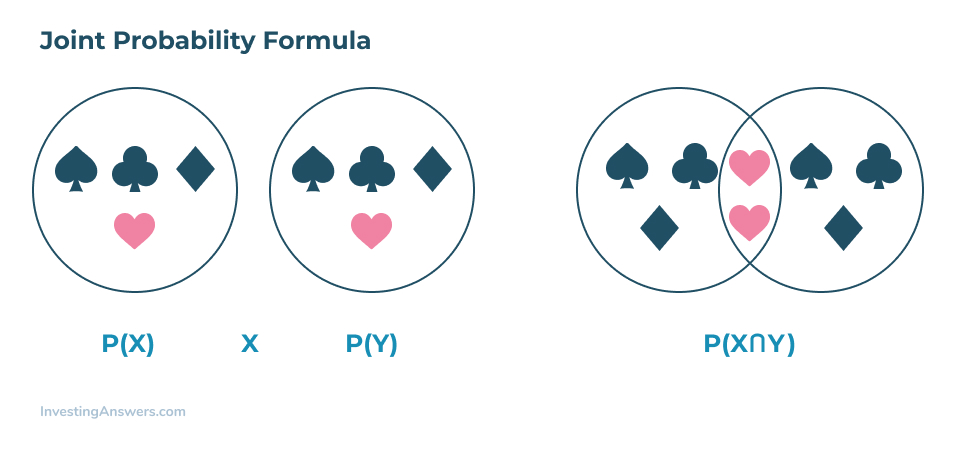
W poniższej formule zobaczysz symbol „∩” używany do reprezentowania przecięcia. Dla bardziej wzrokowców, użycie diagramu Venna jest najlepszym sposobem na zilustrowanie jak dwa wydarzenia mogą się przecinać.
Wzór na prawdopodobieństwo wspólne
Wzór na prawdopodobieństwo wspólne jest następujący:
W tym wzorze, X i Y reprezentują dwa różne przecinające się zdarzenia, a P równa się prawdopodobieństwu połączenia zarówno X jak i Y.
Inne sposoby wyrażenia wzoru na prawdopodobieństwo wspólne to P( X i Y) i P(XY).
Przykład prawdopodobieństwa łącznego #1
Powiedzmy, że chcemy obliczyć prawdopodobieństwo łączne dla rzutu monetą, w którym możemy otrzymać ogon (zdarzenie X), a następnie głowę (zdarzenie Y).
W tym przypadku prawdopodobieństwo zdarzenia X wynosi 50% (lub 0.5), a prawdopodobieństwo zdarzenia Y wynosi również 50%. Teraz możemy wstawić te liczby do wzoru:
P(0.5 x 0.5) = 0.25 lub 25%
To oznacza, że wspólne prawdopodobieństwo otrzymania ogona, a następnie głowy w rzucie monetą wynosi 25%.
Przykład prawdopodobieństwa łącznego #2
Rozrzucasz kostkę i chcesz obliczyć wspólne prawdopodobieństwo wyrzucenia liczby sześć dwa razy z rzędu. Prawdopodobieństwo wyrzucenia szóstki za pierwszym razem wynosi 1/6, ponieważ jest tylko sześć opcji na sześciościennej kostce. To równa się ⅙, czyli 17% (w ułamkach dziesiętnych jest to 0,1666). Tak samo jest za drugim razem.
Korzystając z tej informacji, możemy określić, że łączne prawdopodobieństwo wyrzucenia szóstki za pierwszym i drugim razem będzie następujące:
P(0.1666 x 0.1666) = 0.02777 lub 2.8%
To oznacza, że masz 2.8% prawdopodobieństwo zajścia obu zdarzeń.
Kiedy używać prawdopodobieństwa łącznego
Prawdopodobieństwo łączne jest użyteczne, gdy chcesz zmierzyć dwa niezależne zdarzenia, aby określić czy mogą zajść jednocześnie.
Jakie zastosowanie ma prawdopodobieństwo łączne w odniesieniu do inwestowania?
Prawdopodobieństwo łączne jest użyteczną statystyką dla analityków i statystyków, gdy dwa lub więcej obserwowalnych zjawisk może wystąpić jednocześnie. Na przykład, gdy spadkowi indeksu Dow Jones Industrial Average towarzyszy znaczna utrata wartości dolara.
Można również porównać dwie oddzielne akcje, aby zobaczyć, czy wartość jednej z nich wzrośnie (i czy druga również).