Przekształcenie Fouriera (FT) rozkłada sygnał na częstotliwości, które go tworzą.
Co to znaczy?
Przykładem niech będzie sygnał S1. Mamy sygnał S1.

Jeśli chcemy zmierzyć siłę tego sygnału w jakimś konkretnym czasie. Mierzymy go poprzez jego amplitudę.
Więc amplituda sygnału S1 wynosi 1
Jeśli zrobimy to samo dla innego sygnału i wybierzemy ten sam moment w czasie i zmierzymy jego amplitudę. Niech nam wyjdzie kolejny sygnał S2 jak poniżej

Amplituda sygnału S2 wynosi 2
Co się stanie, gdy wyemitujemy te dwa sygnały w tym samym czasie (S1 i S2) ?
Więc, kiedy emitujemy te dwa sygnały w tym samym momencie czasu, otrzymujemy nowy sygnał, który jest sumą amplitudy tych dwóch sygnałów. Dzieje się tak dlatego, że te dwa sygnały są dodawane do siebie.

Więc, amplituda sygnału S3 = amplituda sygnału S1 + amplituda sygnału S2 = 1 + 2 = 3
Więc amplituda sygnału S3 wynosi 3
Teraz pojawia się ciekawe pytanie :
Jeśli otrzymamy tylko sygnał S3 (który jest sumą sygnałów S1 i S2).Czy możemy odzyskać oryginalne sygnały S1 i S2?
Tak. To jest to, co robi transformata Fouriera. Bierze sygnał i rozkłada go na częstotliwości, które go tworzą.
W naszym przykładzie, transformata Fouriera rozkłada sygnał S3 do jego częstotliwości składowych jak sygnały S1 i S2
Ale, Jak możemy odzyskać oryginalne sygnały? Co transformata Fouriera zrobi dla nas?

Pozwólmy, że trzy sygnały na powyższym rysunku to S1, S2, i S3 i kiedy połączymy te trzy sygnały razem otrzymamy sygnał w kolorze czerwonym, który jest w rzeczywistości sumą trzech sygnałów S1+S2+S3.
To, co robi transformata Fouriera, to rodzaj przeniesienia nas z dziedziny czasu do dziedziny częstotliwości.
W przypadku, jeśli ktoś się zastanawia, co jeśli chcemy wrócić z dziedziny częstotliwości do dziedziny czasu?
Możemy to zrobić za pomocą odwrotnej transformaty Fouriera (IFT). Ale nie będziemy tego omawiać w tym artykule.
Generacja sygnału i przesunięcie fazowe
Jeśli chcemy opisać sygnał, potrzebujemy trzech rzeczy :
- Częstotliwość sygnału, która pokazuje, ile wystąpień w okresie mamy.
- Amplituda, która pokazuje wysokość sygnału lub innymi słowy siłę sygnału.
- Przesunięcie fazowe, gdzie sygnał się zaczyna.
Pierwszy przykład, który wzięliśmy był bardzo prosty, każdy sygnał miał tę samą częstotliwość i różnicę faz i tylko różne amplitudy.
Przyjrzymy się teraz nieco skomplikowany przykład i będziemy patrzeć na poszczególne sygnały z powyższego przykładu, ponieważ w celu lepszego zrozumienia transformaty Fouriera musimy spojrzeć na poszczególne sygnały blisko.
Poniżej znajduje się oryginalny sygnał, który oglądaliśmy powyżej.



Częstotliwość: Jeśli przyjrzymy się bliżej trzem sygnałom, zauważymy, że częstotliwość wszystkich trzech sygnałów jest inna.
Jeśli dla tego samego okresu czasu, w sygnale 1 jest n liczba fal to w sygnale 2 jest 2n liczba fal i odwrotnie.
Faza: Również, gdy przyjrzymy się dokładnie, gdzie właściwie zaczyna się sygnał. Przekonamy się, że podczas gdy sygnał 1 zaczyna się na (0,0), sygnał 2 zaczyna się na (-0,5,0), jeśli prześledzimy falę, aby spotkać się z osią y na 0. Tak więc, na 0 mamy już maksymalną amplitudę sygnału. To jest to, co nazywamy Phase shift.
Amplitude: Wszystkie trzy sygnały mają różne amplitudy, Sygnał 1 ma amplitudę 1, podczas gdy sygnał 2 i sygnał 3 ma amplitudę 2 i 3 odpowiednio.
To wszystko jest uchwycone w eleganckim i super prostym wzorze matematycznym. Tak więc, w powyższych przykładach, jeśli oś x jest określana jako x i oś y jest określana jako y. Możemy wygenerować y jako funkcję t taką, że :

Korzystając z tego wzoru, możemy wygenerować dowolny typ sygnału, który chcemy, a następnie możemy połączyć je razem i bawić się nimi. Na przykład, jeśli połączymy sygnały 1, 2 i 3. otrzymamy sygnał taki jak ten :

Matematyka transformaty Fouriera
Główną ideą transformaty Fouriera jest to, że :
Dowolny ciągły sygnał w dziedzinie czasu może być reprezentowany jednoznacznie i jednoznacznie przez nieskończoną serię sinusoid.
Co to oznacza?
To znaczy, że, Jeśli mamy sygnał i ten sygnał jest generowany przez pewną funkcję x(t) to możemy wymyślić inną funkcję f(t) taką, że :

Więc, Nie ma znaczenia, jak silny jest sygnał, możemy znaleźć funkcję taką jak f(t) która jest sumą nieskończonej serii sinusoid, która faktycznie będzie doskonale reprezentować sygnał.
Teraz pojawia się pytanie, jak znaleźć współczynniki w powyższym równaniu, ponieważ są to wartości, które określą kształt wyjścia, a więc sygnału.
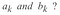
Więc, aby uzyskać te współczynniki używamy transformaty Fouriera, a wynikiem transformaty Fouriera jest grupa współczynników. Tak więc, używamy X(F) do oznaczenia współczynników Fouriera i jest to funkcja częstotliwości, którą otrzymujemy poprzez rozwiązanie całki takiej, że :
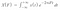
Trudną częścią w tej całce jest tak naprawdę i który oznacza liczbę złożoną. Tak więc, prawdopodobnie pamiętamy, że i² = -1 lub i = √-1. Pomocne może być również zapamiętanie, że formą liczby złożonej jest a + ib . Tak więc, ma ona część rzeczywistą i urojoną.
Ale również, gdy faktycznie rozwiążemy powyższą całkę, otrzymamy te liczby zespolone, gdzie a i b odpowiadają współczynnikom, o które nam chodzi.
Mamy jednak trzy problemy, z którymi musimy się uporać :
- Jak poradzić sobie z
i. - Jak radzić sobie z sygnałami dyskretnymi.
Zacznijmy więc od drugiego z nich.
Aby zrozumieć Dyskretną Transformatę Fouriera, musimy najpierw zrozumieć, jak próbkować sygnał ciągły?
Według Wikipedii, w przetwarzaniu sygnałów, próbkowanie jest redukcją sygnału czasu ciągłego do sygnału czasu dyskretnego. Oto przykład, jak zmienia się postać sygnału wraz ze zmianą częstotliwości próbkowania :
Pozwólmy, aby oryginalny sygnał był sygnałem o amplitudzie dwa i częstotliwości pięć w okresie jednej sekundy :
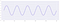
Teraz, gdy zmniejszamy częstotliwość próbkowania, spójrzmy jak zmienia się kształt sygnału:
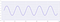
Jak zmniejszamy częstotliwość próbkowania dalej, otrzymujemy :

Więc, wniosek jest taki: Im wyższa częstotliwość próbkowania, tym lepsza jakość sygnału, a także możemy rozróżnić więcej częstotliwości.
Teraz, gdy wiemy, jak próbkować sygnały, przyjrzymy się modyfikacji algorytmów znanych jako Dyskretna Transformacja Fouriera.
Dyskretna transformata Fouriera
Każdy próbkowany sygnał o długości N w dziedzinie czasu może być reprezentowany jednoznacznie i jednoznacznie przez skończoną serię sinusoid.
Więc w naszej nowej definicji nie mamy już do czynienia z nieskończonością.
Jaka jest różnica?
W standardowej transformacie Fouriera użyliśmy funkcji czasu x(t) do wygenerowania sygnału ciągłego. Teraz w przypadku dyskretnym, nie mamy funkcji, mamy zbiór danych, zbiór punktów, które otrzymujemy przez próbkowanie sygnału ciągłego. Więc użyję {x} aby przekazać zbiór danych taki, że zawiera on odczyt z próbkowania taki, że :

A to, co zrobi dla nas Dyskretna Transformata Fouriera (ang. Transformacja Dyskretnego Fouriera zrobi dla nas to, że przekształci zbiór danych {x} w inny zbiór danych {X} który będzie zawierał współczynniki Fouriera takie, że :

Jeśli spojrzymy na definicję transformaty Fouriera, każda X w {X} jest liczbą złożoną i zawiera a i b składowe dla częstotliwości.
Ale, Jak to się dzieje, że dwa zbiory danych {x} i {X} mają tę samą długość?
Jeśli myślimy o tym, co napędza długość {x} dataset jest częstotliwość próbkowania, ponieważ w pewnym okresie czasu liczba punktów danych, które czytam, jest dokładnie częstotliwością próbkowania, prawda? Jeśli pomyślimy o innym zbiorze danych {X} , powiedzieliśmy, że częstotliwość to liczba wystąpień w jednostce czasu. Więc jeśli próbkuję z pewną częstotliwością, nie mogę rozpoznać sygnałów, które mają większą częstotliwość niż częstotliwość próbkowania, tylko dlatego, że nie dostajemy wystarczającej liczby punktów danych.
So, Jeśli mamy sygnały o bardzo wysokich częstotliwościach na bardzo niskiej częstotliwości próbkowania, nie będziemy w stanie rozpoznać tych sygnałów w ogóle. Tak więc, liczba częstotliwości, które możemy rozpoznać poprzez zastosowanie transformaty Fouriera jest w rzeczywistości napędzany przez częstotliwość próbkowania, jak również.
Teraz więc, gdy mamy nasz zbiór danych {x}, otrzymamy {Xk} takie, że jest to element w {X} które są moimi współczynnikami Fouriera takimi, że :
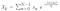
Więc, jest to w zasadzie dyskretna transformata Fouriera. Możemy wykonać to obliczenie i otrzymamy liczbę złożoną w postaci a + ib gdzie mamy dwa współczynniki dla szeregu Fouriera.
Teraz wiemy jak próbkować sygnały i jak zastosować Dyskretną Transformatę Fouriera. Ostatnią rzeczą, którą chcielibyśmy zrobić jest, chcielibyśmy pozbyć się liczby złożonej i ponieważ nie jest ona obsługiwana w mllib lub systemML poprzez użycie czegoś znanego jako formuła Eulera, która stwierdza :
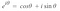
Więc, Jeśli wstawimy wzór Eulera do równania transformaty Fouriera, otrzymamy

Wiemy również, że cos(-θ) = cos(θ) i sin(-θ) = -sin(θ) i jeśli użyjemy tego w powyższym równaniu, równanie może być uproszczone jako :

i tak naprawdę możemy rozbić powyższe równanie na dwie sumy, takie, że :

Teraz, Jeśli porównamy powyższe równanie z równaniem liczby złożonej, która jest a + ib to otrzymamy odpowiednią wartość jako :
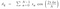
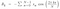
Więc, teraz możemy umieścić te wartości w równaniu f(t) i otrzymać wynik.
Wniosek
W praktyce używamy niewielkiej modyfikacji Dyskretnej Transformaty Fouriera znanej jako Szybka Transformata Fouriera, ponieważ Dyskretna Transformata Fouriera jest bardzo prosta, podstawowa i również powolna. Nie nadaje się do celu, jeśli naprawdę chcemy zrobić coś w środowisku produkcyjnym. Złożoność obliczeniowa Dyskretnej Transformaty Fouriera jest kwadratowa O(n²) i Szybka Transformata Fouriera dla porównania jest quasi-liniowa O(nlogn). Szybka Transformacja Fouriera robi to poprzez wykorzystanie asymetrii w Transformacji Fouriera.