Mechanika Materiałów
Równania i zastosowania naprężeń ścinających
Ogólne naprężenia ścinające:
Wzór na obliczenie średnich naprężeń ścinających to:
gdzie τ = naprężenie ścinające; F = przyłożona siła; A = pole przekroju poprzecznego materiału o powierzchni prostopadłej do wektora przyłożonej siły;
Ścinanie belki:
Ścinanie belki definiuje się jako wewnętrzne naprężenie ścinające belki spowodowane działaniem siły ścinającej przyłożonej do belki.
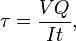gdzie V = całkowita siła ścinająca w danym miejscu; Q = statyczny moment powierzchni; t = grubość materiału w kierunku prostopadłym do ścinania; I = moment bezwładności całego przekroju poprzecznego. Wzór ten znany jest również jako wzór Jourawskiego.Ścinanie w konstrukcji półmonokokowejNaprężenia ścinające w konstrukcji półmonokokowej można obliczyć, idealizując przekrój poprzeczny konstrukcji na zestaw podłużnic (przenoszących tylko obciążenia osiowe) i środników (przenoszących tylko strumienie ścinające). Dzieląc strumień ścinający przez grubość danej części konstrukcji półmonokokowej, uzyskuje się naprężenie ścinające. Tak więc maksymalne naprężenia ścinające wystąpią albo w środniku o maksymalnym przepływie ścinającym, albo o minimalnej grubości.Również konstrukcje w gruncie mogą ulec zniszczeniu na skutek ścinania; np, Ciężar wypełnionej ziemią tamy lub wału może spowodować zapadnięcie się podłoża, jak w przypadku małego osuwiska.Ścinanie przy uderzeniuMaksymalne naprężenie ścinające powstające w litym pręcie okrągłym poddanym uderzeniu jest określone równaniem:
gdzie U = zmiana energii kinetycznej; G = moduł ścinania; V = objętość pręta; oraz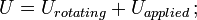 
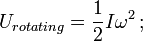
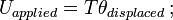
= masowy moment bezwładności; ω = prędkość kątowa.
Naprężenia ścinające w cieczach:
Każda rzeczywista ciecz (w tym ciecze i gazy) poruszająca się wzdłuż granicy ciała stałego doznaje na tej granicy naprężeń ścinających. Warunek braku poślizgu mówi, że prędkość płynu na granicy (względem granicy) wynosi zero, ale na pewnej wysokości od granicy prędkość przepływu musi być równa prędkości płynu. Obszar pomiędzy tymi dwoma punktami jest trafnie nazywany warstwą graniczną. Dla wszystkich płynów newtonowskich w przepływie laminarnym naprężenie ścinające jest proporcjonalne do prędkości odkształcenia płynu, gdzie lepkość jest stałą proporcjonalności. Jednak w przypadku płynów nienewtonowskich nie jest to już prawdą, ponieważ lepkość w tych płynach nie jest stała. Naprężenie ścinające jest przenoszone na granicę w wyniku utraty prędkości. Naprężenie ścinające, dla płynu newtonowskiego, na elemencie powierzchni równoległym do płaskiej płyty, w punkcie y, jest dane przez:
gdzie μ jest lepkością dynamiczną płynu; u jest prędkością płynu wzdłuż granicy; y jest wysokością nad granicą. W szczególności, naprężenie ścinające w ścianie jest zdefiniowane jako: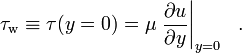 
W przypadku wiatru, naprężenie ścinające na granicy nazywane jest naprężeniem wiatrowym.
1. Timoshenko, Stephen P. (1983), History of Strength of Material, Courier Dover Publications, s. 141, ISBN 0486611876, http://books.google.com/?id=tkScQmyhsb8C .
2. Day, Michael A. (2004), The no-slip condition of fluid dynamics, Springer Netherlands, s. 285-296, ISSN (Print) 1572-8420 (Online) 0165-0106 (Print) 1572-8420 (Online), http://www.springerlink.com/content/k1m4t1p02m778u88/.
3. Naqwi, A. A.; Reynolds, W. C. (jan 1987), „Dual cylindrical wave laser-Doppler method for measurement of skin friction in fluid flow”, NASA STI/Recon Technical Report N 87
4. Große, S.; Schröder, W. (2009), „Two-Dimensional Visualization of Turbulent Wall Shear Stress Using Micropillars”, AIAA Journal 47 (2): 314-321, Bibcode 2009AIAAJ..47..314G, doi:10.2514/1.36892
5. Große, S.; Schröder, W. (2008), „Dynamic Wall-Shear Stress Measurements in Turbulent Pipe Flow using the Micro-Pillar Sensor MPS³”, International Journal of Heat and Fluid Flow 29 (3): 830-840, doi:10.1016/j.ijheatfluidflow.2008.01.008
4.