
Regresja logistyczna znalazła zastosowanie w naukach biologicznych na początku XX wieku. Następnie została wykorzystana w wielu zastosowaniach w naukach społecznych. Regresja logistyczna jest używana, gdy zmienna zależna (cel) jest kategoryczna.
Na przykład,
- Aby przewidzieć, czy e-mail jest spamem (1) czy (0)
- Czy guz jest złośliwy (1) czy nie (0)
Rozważmy scenariusz, w którym musimy sklasyfikować, czy e-mail jest spamem czy nie. Jeśli użyjemy regresji liniowej do tego problemu, istnieje potrzeba ustanowienia progu, na podstawie którego można dokonać klasyfikacji. Powiedzmy, że jeśli rzeczywista klasa jest złośliwa, przewidywana wartość ciągła 0,4, a wartość progowa wynosi 0,5, punkt danych zostanie sklasyfikowany jako niezłośliwy, co może prowadzić do poważnych konsekwencji w czasie rzeczywistym.
Z tego przykładu można wywnioskować, że regresja liniowa nie jest odpowiednia dla problemu klasyfikacji. Regresja liniowa jest nieograniczona, a to daje regresję logistyczną. Ich wartość ściśle mieści się w przedziale od 0 do 1.
Prosta regresja logistyczna
(Pełny kod źródłowy: https://github.com/SSaishruthi/LogisticRegression_Vectorized_Implementation/blob/master/Logistic_Regression.ipynb)
Model
Wyjście = 0 lub 1
Hipoteza => Z = WX + B
hΘ(x) = sigmoida (Z)
Sigmoida. Funkcja

Jeśli 'Z' zmierza do nieskończoności, Y(predicted) stanie się 1, a jeśli 'Z' zmierza do ujemnej nieskończoności, Y(predicted) stanie się 0.
Analiza hipotezy
Wynikiem hipotezy jest szacowane prawdopodobieństwo. Jest to używane do wnioskowania, jak pewnie może przewidywana wartość być rzeczywista wartość, gdy podano dane wejściowe X. Rozważmy poniższy przykład,
X = =
Na podstawie wartości x1, powiedzmy, że uzyskaliśmy szacowane prawdopodobieństwo 0,8. Oznacza to, że istnieje 80% szans, że wiadomość e-mail będzie spamem.
Matematycznie można to zapisać jako,

To uzasadnia nazwę „regresja logistyczna”. Dane są dopasowywane do modelu regresji liniowej, na które następnie działa funkcja logistyczna przewidująca docelową kategoryczną zmienną zależną.
Typy regresji logistycznej
1. Binarna regresja logistyczna
Kategoryczna odpowiedź ma tylko dwa 2 możliwe wyniki. Przykład: Spam lub Nie
2. wielomianowa regresja logistyczna
Trzy lub więcej kategorii bez uporządkowania. Przykład: Przewidywanie, które jedzenie jest bardziej preferowane (Veg, Non-Veg, Vegan)
3. Regresja logistyczna porządkowa
Trzy lub więcej kategorii z porządkowaniem. Przykład: Ocena filmu od 1 do 5
Decision Boundary
Aby przewidzieć, do której klasy należą dane, można ustalić próg. W oparciu o ten próg, otrzymane szacunkowe prawdopodobieństwo jest klasyfikowane do klas.
Na przykład, jeśli predicted_value ≥ 0.5, to sklasyfikuj email jako spam, w przeciwnym razie jako nie spam.
Granica decyzji może być liniowa lub nieliniowa. Kolejność wielomianów może być zwiększona, aby uzyskać złożoną granicę decyzji.
Funkcja kosztu
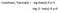
Dlaczego funkcja kosztu, która została użyta dla liniowej nie może być użyta dla logistycznej?
Regresja liniowa używa błędu średniokwadratowego jako funkcji kosztu. Jeśli zostanie ona użyta w regresji logistycznej, będzie to niewypukła funkcja parametrów (theta). Gradient descent będzie zbiegał do minimum globalnego tylko wtedy, gdy funkcja jest wypukła.

Wyjaśnienie funkcji kosztu


Uproszczona funkcja kosztu

Dlaczego taka funkcja kosztów?
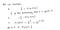
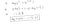
Ta ujemna funkcja wynika z tego, że kiedy trenujemy, musimy zmaksymalizować prawdopodobieństwo poprzez minimalizację funkcji straty. Zmniejszenie kosztu spowoduje zwiększenie maksymalnego prawdopodobieństwa przy założeniu, że próbki są pobierane z identycznie niezależnego rozkładu.
Odkrywanie wzoru dla algorytmu zstępującego gradientu


Implementacja w języku Python
def weightInitialization(n_features):
w = np.zeros((1,n_features))
b = 0
return w,bdef sigmoid_activation(result):
final_result = 1/(1+np.exp(-result))
return final_result
def model_optimize(w, b, X, Y):
m = X.shape
#Prediction
final_result = sigmoid_activation(np.dot(w,X.T)+b)
Y_T = Y.T
cost = (-1/m)*(np.sum((Y_T*np.log(final_result)) + ((1-Y_T)*(np.log(1-final_result)))))
#
#Gradient calculation
dw = (1/m)*(np.dot(X.T, (final_result-Y.T).T))
db = (1/m)*(np.sum(final_result-Y.T))
grads = {"dw": dw, "db": db}
return grads, costdef model_predict(w, b, X, Y, learning_rate, no_iterations):
costs =
for i in range(no_iterations):
#
grads, cost = model_optimize(w,b,X,Y)
#
dw = grads
db = grads
#weight update
w = w - (learning_rate * (dw.T))
b = b - (learning_rate * db)
#
if (i % 100 == 0):
costs.append(cost)
#print("Cost after %i iteration is %f" %(i, cost))
#final parameters
coeff = {"w": w, "b": b}
gradient = {"dw": dw, "db": db}
return coeff, gradient, costsdef predict(final_pred, m):
y_pred = np.zeros((1,m))
for i in range(final_pred.shape):
if final_pred > 0.5:
y_pred = 1
return y_pred
Koszt vs Number_of_Iterations

Dokładność trenu i testu systemu wynosi 100%
Ta implementacja dotyczy binarnej regresji logistycznej. W przypadku danych zawierających więcej niż 2 klasy, należy użyć regresji softmax.
To jest post edukacyjny i zainspirowany kursem głębokiego uczenia prof. Andrew Ng.
Pełny kod : https://github.com/SSaishruthi/LogisticRegression_Vectorized_Implementation/blob/master/Logistic_Regression.ipynb