- Zachowanie średniej z próby (x-bar)
- Rozkład próbkowania średniej z próby
Zachowanie się średniej z próby (x-bar)
Do tej pory omówiliśmy zachowanie statystyki p-hat, proporcji próbki, w stosunku do parametru p, proporcji populacji (gdy zmienna zainteresowania jest kategoryczna).
Przejdziemy teraz do zbadania zachowania się statystyki x-bar, średniej z próby, względem parametru μ (mu), średniej populacji (gdy zmienna jest ilościowa).
Zacznijmy od przykładu.
Przykład 9: Behavior of Sample Means
Wagi urodzeniowe są rejestrowane dla wszystkich niemowląt w pewnym mieście. Średnia waga urodzeniowa wynosi 3500 gramów, µ = mu = 3500 g. Jeśli zbierzemy wiele losowych prób 9 dzieci naraz, jak myślisz, jak zachowają się średnie z prób?
Ponownie, pracujemy ze zmienną losową, ponieważ próby losowe będą miały średnie, które zmieniają się nieprzewidywalnie w krótkim okresie, ale wykazują prawidłowości w długim okresie.
W oparciu o naszą intuicję i to, czego nauczyliśmy się o zachowaniu proporcji w próbce, możemy oczekiwać następujących rzeczy na temat rozkładu średnich z próbki:
Centrum: Niektóre średnie próbki będą po stronie niskich wartości – powiedzmy 3000 gramów lub więcej – podczas gdy inne będą po stronie wysokich wartości – powiedzmy 4000 gramów lub więcej. Przy wielokrotnym pobieraniu próbek możemy oczekiwać, że próby losowe będą uśrednione do średniej populacji wynoszącej 3500 g. Innymi słowy, średnia średnich z prób wyniesie µ (mu), tak jak średnia proporcji z prób wyniosła p.
Rozrzut: Dla dużych prób możemy oczekiwać, że średnie z próby nie będą zbytnio odbiegać od średniej dla populacji wynoszącej 3500. Średnie z próby niższe niż 3,000 lub wyższe niż 4,000 mogą być zaskakujące. W przypadku mniejszych prób, bylibyśmy mniej zaskoczeni przez średnie z próby, które różniłyby się znacznie od 3 500. Innymi słowy, moglibyśmy oczekiwać większej zmienności w średnich z próby dla mniejszych prób. Tak więc wielkość próby będzie ponownie odgrywać rolę w rozkładzie miar próby, tak jak to zaobserwowaliśmy dla proporcji próby.
Kształt: Średnie z próby najbliższe 3500 będą najczęstsze, przy czym średnie z próby odległe od 3500 w każdym kierunku będą stopniowo mniej prawdopodobne. Innymi słowy, kształt rozkładu średnich z próby powinien być wybrzuszony w środku i zwężać się na końcach z kształtem, który jest w pewnym sensie normalny. To, ponownie, jest to, co widzieliśmy, gdy patrzyliśmy na proporcje próby.
Komentarz:
- Rozkład wartości średniej z próby (x-bar) w powtarzających się próbach nazywamy rozkładem próbkowania x-bar.
Przyjrzyjrzyjrzyjmy się symulacji:
Wyniki, które znaleźliśmy w naszych symulacjach, nie są zaskakujące. Zaawansowana teoria prawdopodobieństwa potwierdza to twierdząc, co następuje:
Rozkład próbkowania średniej próbki
Jeśli powtarzające się próbki losowe o danym rozmiarze n są pobierane z populacji wartości dla zmiennej ilościowej, gdzie średnia populacji jest μ (mu) i odchylenie standardowe populacji jest σ (sigma) wtedy średnia wszystkich średnich próbek (x-bars) jest średnią populacji μ (mu).
As for the spread of all sample means, theory dictates the behavior much more precisely than saying that there is less spread for larger samples. W rzeczywistości, odchylenie standardowe wszystkich średnich z próby jest bezpośrednio związane z wielkością próby, n, jak wskazano poniżej.
![]()
Ponieważ pierwiastek kwadratowy z wielkości próby n pojawia się w mianowniku, odchylenie standardowe maleje wraz ze wzrostem wielkości próby.
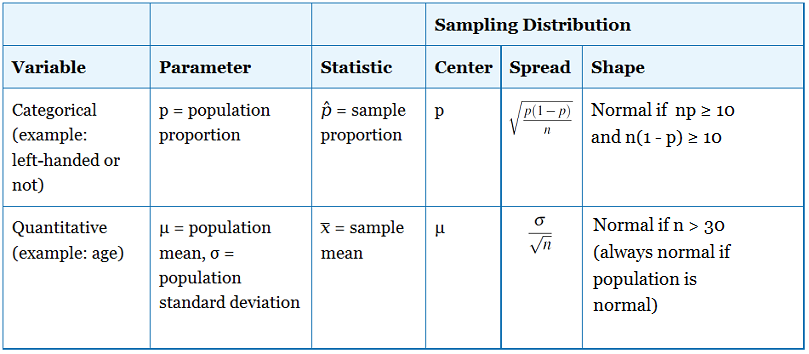
Porównajmy i skontrastujmy to, co teraz wiemy o rozkładach próbkowania dla średnich i proporcji próbkowych.

Teraz zbadamy kształt rozkładu próbkowania średnich próbkowych. Kiedy omawialiśmy rozkład proporcji w próbie, powiedzieliśmy, że rozkład ten jest w przybliżeniu normalny, jeśli np ≥ 10 i n(1 – p) ≥ 10. Innymi słowy, mieliśmy wskazówkę opartą na wielkości próby dla określenia warunków, w których możemy użyć normalnych obliczeń prawdopodobieństwa dla proporcji próby.
Kiedy rozkład średnich z próby będzie w przybliżeniu normalny? Czy zależy to od wielkości próby?
Wydaje się rozsądne, że populacja o rozkładzie normalnym będzie miała średnie z próby, które są normalnie rozłożone nawet dla bardzo małych prób. Widzieliśmy to w poprzedniej symulacji z próbkami o rozmiarze 10.
Co się stanie, jeśli rozkład zmiennej w populacji jest mocno skośny? Czy średnie z próby również mają rozkład skośny? Jeśli weźmiemy naprawdę duże próbki, to czy średnie z próbek staną się bardziej normalnie rozłożone?
W następnej symulacji zbadamy te pytania.
Podsumowując, rozkład średnich próbkowych będzie w przybliżeniu normalny tak długo, jak długo wielkość próbki jest wystarczająco duża. To odkrycie jest prawdopodobnie najważniejszym wynikiem przedstawianym we wstępnych kursach statystyki. Jest ono formalnie określone jako Centralne Twierdzenie Graniczne.
Będziemy polegać na Centralnym Twierdzeniu Granicznym ponownie i ponownie w celu wykonania normalnych obliczeń prawdopodobieństwa, kiedy używamy średnich z próby do wyciągnięcia wniosków na temat średniej populacji. Teraz wiemy, że możemy to zrobić nawet jeśli rozkład populacji nie jest normalny.
Jak dużej wielkości próby potrzebujemy, aby założyć, że średnie z próby będą miały rozkład normalny? Cóż, to naprawdę zależy od rozkładu populacji, jak widzieliśmy w symulacji. Ogólna zasada jest taka, że próbki o rozmiarze 30 lub większym będą miały w miarę normalny rozkład niezależnie od kształtu rozkładu zmiennej w populacji.
Komentarz:
- Dla zmiennych kategorycznych, nasze twierdzenie, że proporcje próbki są w przybliżeniu normalne dla wystarczająco dużego n jest w rzeczywistości specjalnym przypadkiem Centralnego Twierdzenia Granicznego. W tym przypadku myślimy o danych jako o 0 i 1, a „średnia” z tych 0 i 1 jest równa proporcji, o której mówiliśmy.
Zanim przepracujemy kilka przykładów, porównajmy i skontrastujmy to, co teraz wiemy o rozkładach próbkowania dla średnich i proporcji próbkowych.
Przykład 10: Using the Sampling Distribution of x-bar
Wielkość gospodarstwa domowego w Stanach Zjednoczonych ma średnią 2,6 osoby i odchylenie standardowe 1,4 osoby. Powinno być jasne, że rozkład ten jest skośny w prawo, ponieważ najmniejszą możliwą wartością jest gospodarstwo domowe składające się z 1 osoby, ale największe gospodarstwa domowe mogą być naprawdę bardzo duże.
(a) Jakie jest prawdopodobieństwo, że losowo wybrane gospodarstwo domowe liczy więcej niż 3 osoby?
Przybliżenie normalne nie powinno być tutaj użyte, ponieważ rozkład wielkości gospodarstw domowych byłby znacznie skośny w prawo. Nie mamy wystarczającej ilości informacji, aby rozwiązać ten problem.
(b) Jakie jest prawdopodobieństwo, że średnia wielkość próby losowej 10 gospodarstw domowych jest większa niż 3?
Pod względem standardów, 10 jest małą wielkością próby. Centralne Twierdzenie Graniczne nie gwarantuje, że średnia z próby pochodząca z populacji skośnej będzie w przybliżeniu normalna, chyba że wielkość próby jest duża.
(c) Jakie jest prawdopodobieństwo, że średnia wielkość próby losowej 100 gospodarstw domowych jest większa niż 3?
Teraz możemy powołać się na Centralne Twierdzenie Graniczne: nawet jeśli rozkład wielkości gospodarstwa domowego X jest skośny, rozkład średniej wielkości gospodarstwa domowego (x-bar) jest w przybliżeniu normalny dla dużej próby, takiej jak 100. Jego średnia jest taka sama jak średnia populacji, 2.6, a jego odchylenie standardowe jest odchyleniem standardowym populacji podzielonym przez pierwiastek kwadratowy z liczebności próby:

Do znalezienia
![]()
Standaryzujemy 3 do z-score poprzez odjęcie średniej i podzielenie wyniku przez odchylenie standardowe (średniej z próby). Następnie możemy znaleźć prawdopodobieństwo używając standardowego normalnego kalkulatora lub tabeli.

Gospodarstwa domowe liczące więcej niż 3 osoby są oczywiście dość powszechne, ale byłoby niezwykle niezwykłe, aby średnia wielkość próby 100 gospodarstw domowych była większa niż 3.
Celem następnej aktywności jest ćwiczenie z przewodnikiem w znajdowaniu rozkładu próbkowania średniej z próby (x-bar) i wykorzystanie go do poznania prawdopodobieństwa uzyskania pewnych wartości x-bar.