„Stopień” może oznaczać kilka rzeczy w matematyce:
- W geometrii stopień (°) jest sposobem mierzenia kątów,
- Ale tutaj przyjrzymy się temu, co stopień oznacza w algebrze.
W algebrze „Stopień” jest czasami nazywany „Porządkiem”
Stopień wielomianu (z jedną zmienną)
Wielomian wygląda tak:
przykład wielomianu
ten ma 3 wyrazy
Stopień (dla wielomianu z jedną zmienną, jak x) to:
największy wykładnik tej zmiennej.
Więcej przykładów:
| 4x | Stopień wynosi 1 (zmienna bez wykładnika w rzeczywistości ma wykładnik równy 1) |
|
| 4×3 – x + 3 | The Degree is 3 (biggest exponent of x) | |
| . | ||
| x2 + 2×5 – x | Stopień wynosi 5 (największy wykładnik x) | |
| z2 – z + 3 | Stopień wynosi 2 (największy wykładnik z) |
Nazwy stopni
Kiedy znamy stopień możemy nadać mu nazwę!
| Stopień | Nazwa | Przykład |
|---|---|---|
| 0 | Constant | 7 |
| 1 | Linear | x+3 |
| 2 | Quadratic | x2-x+2 |
| 3 | Cubic | x3-x2+5 |
| 4 | Quartic | 6×4-x3+x-2 |
| 5 | Quintic | x5-3×3+x2+8 |
Przykład: y = 2x + 7 ma stopień 1, więc jest to równanie liniowe
Przykład: 5w2 – 3 ma stopień 2, więc jest to równanie kwadratowe
Równania wyższego rzędu są zwykle trudniejsze do rozwiązania:
- Równania liniowe są łatwe do rozwiązania
- Równania kwadratowe są trochę trudniejsze do rozwiązania
- Równania sześcienne są znowu trudniejsze, ale są wzory, aby pomóc
- Równania kwarcowe mogą być również rozwiązane, ale wzory są bardzo skomplikowane
- Równania kwintowe nie mają wzorów, a czasami mogą być nierozwiązywalne!
Stopień wielomianu z więcej niż jedną zmienną
Gdy wielomian ma więcej niż jedną zmienną, musimy przyjrzeć się każdemu z członów. Określenia są oddzielone znakami + lub -:
Przykład wielomianu
z więcej niż jedną zmienną
Dla każdego wyrazu:
- Znajdź stopień dodając wykładniki każdej zmiennej w nim występującej,
Największy taki stopień jest stopniem wielomianu.
Przykład: jaki jest stopień tego wielomianu:
Sprawdzenie każdego z członów:
- 5xy2 ma stopień 3 (x ma wykładnik 1, y ma 2, i 1+2=3)
- 3x ma stopień 1 (x ma wykładnik 1)
- 5y3 ma stopień 3 (y ma wykładnik 3)
- 3 ma stopień 0 (brak zmiennej)
Największym stopniem spośród tych jest 3 (w rzeczywistości dwa terminy mają stopień 3), więc wielomian ma stopień 3
Przykład: jaki jest stopień tego wielomianu:
4z3 + 5y2z2 + 2yz
Sprawdzenie każdego z członów:
- 4z3 ma stopień 3 (z ma wykładnik 3)
- 5y2z2 ma stopień 4 (y ma wykładnik 2, z ma 2, a 2+2=4)
- 2yz ma stopień 2 (y ma wykładnik 1, z ma 1, i 1+1=2)
Największym stopniem z tych jest 4, więc wielomian ma stopień 4
Writing it Down
Zamiast mówić „stopień (czegokolwiek) jest 3” zapiszemy to w ten sposób:
![]()
Gdy wyrażenie jest ułamkiem
Możemy obliczyć stopień wyrażenia racjonalnego (takiego, które ma postać ułamka) biorąc stopień z góry (licznik) i odejmując stopień z dołu (mianownik).
Tutaj są trzy przykłady:
Obliczanie innych typów wyrażeń
Ostrzeżenie: Advanced Ideas Ahead!
Czasami możemy obliczyć stopień wyrażenia dzieląc …
- logarytm funkcji przez
- logarytm zmiennej
… a następnie robić to dla coraz większych wartości, aby zobaczyć, gdzie „zmierza” odpowiedź.
(Bardziej poprawnie powinniśmy opracować Limit do nieskończoności ln(f(x))/ln(x), ale chcę zachować prostotę).
|
Uwaga: „ln” jest funkcją logarytmu naturalnego. |
 |
Tutaj przykład:
Przykład: Jaki jest stopień liczby (3 plus pierwiastek kwadratowy z x) ?
Spróbujmy zwiększać wartości x:
| x | ln( |
ln(x) | ln(x) | ln( / ln(x) |
|---|---|---|---|---|
| 2 | 1.48483 | 0.69315 | 2.1422 | |
| 4 | 1.60944 | 1.38629 | 1.1610 | |
| 10 | 1.81845 | 2.30259 | 0.7897 | |
| 100 | 2.56495 | 4.60517 | 0.5570 | |
| 1,000 | 3.54451 | 6.90776 | 0.5131 | |
| 10,000 | 4.63473 | 9.21034 | 0.5032 | |
| 100,000 | 5.76590 | 11.51293 | 0.5008 | |
| 1,000,000 | 6.91075 | 13.81551 | 0.5002 |
Patrząc na tabelę:
- jak x staje się większe to ln(
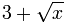 ) / ln(x) coraz bardziej zbliża się do 0,5
) / ln(x) coraz bardziej zbliża się do 0,5
Więc Stopień wynosi 0.5 (innymi słowy 1/2)
(Uwaga: to się ładnie zgadza z x½ = pierwiastek kwadratowy z x, patrz Wykładniki ułamkowe)
Niektóre wartości stopni
| Wyrażenie | Stopień |
|---|---|
| log(x) | 0 |
| ex | ∞ |
| 1/x | -1 |
| 1/2 |



