Guinguette Marais Poitevin

Spis treści:

• Co to jest test T?
• The T Score
• T Values and P Values
• Calculating the T Test
• What is a Paired T Test (Paired Samples T Test)?

What is a T test?

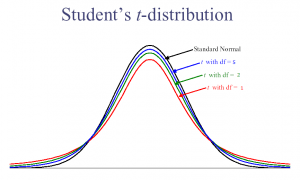
Różne stopnie swobody dla testu T Studenta.

Test t mówi, jak znaczące są różnice między grupami; Innymi słowy, pozwala dowiedzieć się, czy te różnice (mierzone w średnich) mogły się zdarzyć przez przypadek.

Bardzo prosty przykład: Powiedzmy, że masz przeziębienie i próbujesz naturopatycznego remedium. Twoje przeziębienie trwa kilka dni. Następnym razem, gdy masz przeziębienie, kupujesz farmaceutyk bez recepty i przeziębienie trwa tydzień. Ankietujesz swoich przyjaciół i wszyscy mówią ci, że ich przeziębienia trwały krócej (średnio 3 dni), kiedy zażywali homeopatyczny środek. To, co naprawdę chcesz wiedzieć, to czy te wyniki są powtarzalne? Test t może Ci to powiedzieć porównując średnie dwóch grup i dając Ci znać o prawdopodobieństwie wystąpienia tych wyników przez przypadek.

Inny przykład: Testy t-Studenta mogą być używane w prawdziwym życiu do porównywania średnich. Na przykład, firma farmaceutyczna może chcieć przetestować nowy lek na raka, aby dowiedzieć się, czy poprawia on oczekiwaną długość życia. W eksperymencie zawsze istnieje grupa kontrolna (grupa, która otrzymuje placebo, czyli „cukrową pigułkę”). Grupa kontrolna może wykazywać średnią długość życia +5 lat, podczas gdy grupa przyjmująca nowy lek może mieć średnią długość życia +6 lat. Wydawałoby się, że lek może działać. Ale to może być spowodowane fluke. Aby to sprawdzić, badacze użyliby testu t-Studenta, aby dowiedzieć się, czy wyniki są powtarzalne dla całej populacji.

Wciąż masz problemy? Chegg.com połączy Cię z wirtualnym korepetytorem (a pierwsze 30 minut jest darmowe!).

Wynik T.

Wynik t to stosunek różnicy między dwiema grupami do różnicy wewnątrz grup. Im większy wynik t, tym większa różnica między grupami. Im mniejszy wynik t, tym większe podobieństwo między grupami. Wynik t równy 3 oznacza, że grupy różnią się od siebie trzykrotnie bardziej niż w obrębie jednej grupy. Kiedy przeprowadzasz test t, im większa jest wartość t, tym bardziej prawdopodobne jest, że wyniki są powtarzalne.

• Duży wynik t mówi, że grupy są różne.
• Mały wynik t mówi, że grupy są podobne.

Wartości t i wartości P

Jak duża wartość jest „wystarczająco duża”? Każda wartość t ma swoją wartość p. Wartość p to prawdopodobieństwo, że wyniki z twojej próbki danych pojawiły się przez przypadek. Wartości p mieszczą się w przedziale od 0% do 100%. Zazwyczaj zapisuje się je w postaci dziesiętnej. Na przykład, wartość p równa 5% wynosi 0,05. Niskie wartości p są dobre; Wskazują one, że dane nie powstały przypadkowo. Na przykład, wartość p równa .01 oznacza, że istnieje tylko 1% prawdopodobieństwa, że wyniki eksperymentu są przypadkowe. W większości przypadków, wartość p równa 0.05 (5%) jest akceptowana jako oznaczająca, że dane są ważne.

Obliczanie statystyki / Typy testów

Istnieją trzy główne typy testów t:

• Test t dla prób niezależnych porównuje średnie dla dwóch grup.
• Test t-parowanych próbek porównuje średnie z tej samej grupy w różnym czasie (powiedzmy w odstępie jednego roku).
• Test t-jednej próbki testuje średnią pojedynczej grupy w stosunku do znanej średniej.

Prawdopodobnie nie chcesz obliczać testu ręcznie (matematyka może stać się bardzo niechlujna, ale jeśli nalegasz, możesz znaleźć kroki dla testu t niezależnych próbek tutaj.

Użyj następujących narzędzi do obliczenia testu t:
Jak zrobić test T w Excelu.
Test T w SPSS.
Rozkład T na TI 89.
Rozkład T na TI 83.

Co to jest test T par (test T parowanych próbek / test T próbek zależnych)?

Test t par (zwany również testem t par skorelowanych, testem t par lub testem t próbek zależnych) polega na przeprowadzeniu testu t na próbkach zależnych. Zależne próbki są zasadniczo połączone – są to testy na tej samej osobie lub rzeczy. Na przykład:

• Koszty MRI kolana w dwóch różnych szpitalach,
• Dwa testy na tej samej osobie przed i po treningu,
• Dwa pomiary ciśnienia krwi na tej samej osobie przy użyciu różnych urządzeń.

Kiedy wybrać test T dla par / test T dla parowanych próbek / test T dla próbek zależnych

Wybierz test t dla par, jeśli masz dwa pomiary tego samego przedmiotu, osoby lub rzeczy. Powinieneś również wybrać ten test, jeśli masz dwa przedmioty, które są mierzone z unikalnym warunkiem. Na przykład, możesz mierzyć bezpieczeństwo samochodów w dziale badań i testów pojazdów i poddawać je serii testów zderzeniowych. Chociaż producenci są różni, możesz poddawać je tym samym warunkom.

W przypadku „zwykłego” testu t dla dwóch próbek porównujemy średnie dla dwóch różnych próbek. Na przykład, można przetestować dwie różne grupy pracowników obsługi klienta na teście związanym z biznesem lub przetestować studentów z dwóch uniwersytetów pod kątem ich umiejętności posługiwania się językiem angielskim. Jeśli weźmiesz losową próbkę każdej grupy osobno i będą one miały różne warunki, twoje próbki są niezależne i powinieneś przeprowadzić test t dla prób niezależnych (zwany również testem między próbkami lub testem bez par).

Hipoteza zerowa dla testu t dla prób niezależnych to μ1 = μ2. Innymi słowy, zakłada ona, że średnie są równe. W przypadku sparowanego testu t hipotezą zerową jest to, że różnica pomiędzy dwoma testami jest równa (H0: μd = 0). Różnica między tymi dwoma testami jest bardzo subtelna; to, który z nich wybierzesz, zależy od metody zbierania danych.

Test t parowanych próbek przeprowadzony ręcznie

Przykładowe pytanie: Oblicz ręcznie sparowany test t dla następujących danych: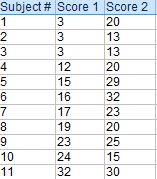

Krok 1: Odejmij każdy wynik Y od każdego wyniku X.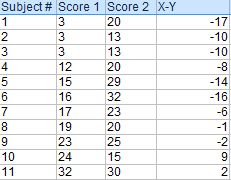

Krok 2: Zsumuj wszystkie wartości z kroku 1.
Odłóż tę liczbę na chwilę na bok.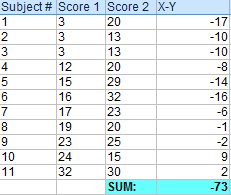

Krok 3: Zsumuj różnice z kroku 1.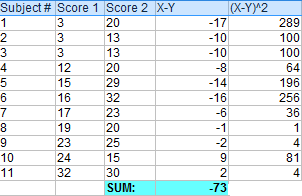

Krok 4: Zsumuj wszystkie podniesione do kwadratu różnice z kroku 3.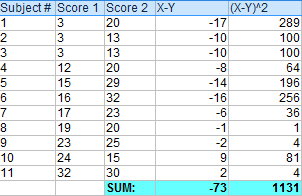

Krok 5: Użyj następującego wzoru, aby obliczyć t-score: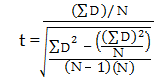

• ΣD: Suma różnic (Suma X-Y z kroku 2)
• ΣD2: Suma różnic podniesionych do kwadratu (z kroku 4)
• (ΣD)2: Suma różnic (z kroku 2), podniesiona do kwadratu.

Jeśli nie jesteś zaznajomiony z Σ możesz chcieć najpierw przeczytać o notacji sumowania.

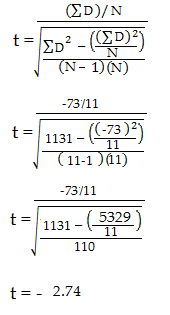
Krok 6: Odejmij 1 od wielkości próby, aby uzyskać stopnie swobody. Mamy 11 elementów, więc 11-1 = 10.

Krok 7: Znajdź wartość p w tabeli t, używając stopni swobody z kroku 6. Jeśli nie masz określonego poziomu alfa, użyj 0,05 (5%). Dla tego przykładowego problemu, przy df = 10, wartość t wynosi 2.228.

Krok 8: Porównaj wartość w tabeli t z kroku 7 (2.228) z obliczoną wartością t (-2.74). Obliczona wartość t jest większa niż wartość tabelaryczna na poziomie alfa .05. Wartość p jest mniejsza niż poziom alfa: p <.05. Możemy odrzucić hipotezę zerową, że nie ma różnicy między średnimi.

Uwaga: Możesz zignorować znak minus podczas porównywania dwóch wartości t, ponieważ &pm; wskazuje kierunek; wartość p pozostaje taka sama dla obu kierunków.

Sprawdź nasz kanał YouTube, aby uzyskać więcej pomocy i wskazówek dotyczących statystyk!

Goulden, C. H. Methods of Statistical Analysis, 2nd ed. New York: Wiley, s. 50-55, 1956.

—————————————————————————–

Potrzebujesz pomocy z zadaniem domowym lub pytaniem testowym? Dzięki Chegg Study możesz uzyskać rozwiązania krok po kroku od eksperta w danej dziedzinie. Pierwsze 30 minut z korepetytorem Chegg jest bezpłatne!