
W poprzednim artykule, zbadaliśmy Analizę Regresji Liniowej i jej zastosowanie w analizie finansowej i modelowaniu. Możesz przeczytać nasz artykuł Analiza regresji w modelowaniu finansowym, aby uzyskać więcej wglądu w koncepcje statystyczne wykorzystywane w tej metodzie i gdzie znajduje ona zastosowanie w finansach.
W tym artykule przyjrzymy się w praktyce modelowaniu modelu regresji wielorakiej dla Produktu Krajowego Brutto (PKB) danego kraju.
Zanim zacznę, pozwól mi dodać krótkie zastrzeżenie. Nie jestem statystykiem i nie twierdzę, że wybrane zmienne zależne i niezależne są właściwymi wyborami analitycznymi. Artykuł ma na celu pokazanie, jak uruchomić Regresję wieloraką w Excelu i zinterpretować dane wyjściowe, a nie nauczanie o ustalaniu założeń modelu i wyborze najodpowiedniejszych zmiennych.
Gdy mamy to już za sobą i oczekiwania są ustalone, otwórzmy Excela i zaczynajmy!
Do tego ćwiczenia uzyskamy dane publiczne z Eurostatu, bazy danych statystycznych Komisji Europejskiej. Dla Twojej wygody wszystkie istotne dane źródłowe znajdują się w pliku modelu, który możesz pobrać poniżej. Zachowałem również linki do tabel źródłowych, abyś mógł je dalej badać, jeśli chcesz.
Zbiór danych UE daje nam informacje dla wszystkich państw członkowskich Unii. Jako wielki fan Herkulesa Poirot Agathy Christie, skierujmy naszą uwagę na Belgię.
Jak widać w poniższej tabeli, mamy dziewiętnaście obserwacji naszej zmiennej docelowej (PKB), jak również trzy zmienne predykcyjne:
- X1 – Wydatki na edukację w mln.
- X2 – Stopa bezrobocia jako % siły roboczej;
- X3 – Wynagrodzenia pracownicze w mln.

Jeszcze zanim uruchomimy nasz model regresji, zauważamy pewne zależności w naszych danych. Patrząc na rozwój w poszczególnych okresach, możemy założyć, że PKB rośnie wraz z wydatkami na edukację i wynagrodzenia pracowników.
Wykonanie wielokrotnej regresji liniowej
Istnieją sposoby na obliczenie wszystkich istotnych statystyk w Excelu przy użyciu formuł. Ale jest to o wiele łatwiejsze dzięki pakietowi narzędzi do analizy danych, który możesz włączyć na karcie Deweloper -> Dodatki do Excela.
Spójrz na kartę Dane, a po prawej stronie zobaczysz narzędzie do analizy danych w sekcji Analizuj.
Uruchom je i wybierz Regresję ze wszystkich opcji. Uwaga, używamy tego samego menu zarówno dla prostych (pojedynczych), jak i wielokrotnych modeli regresji liniowej.
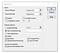
Teraz czas na określenie zakresów i ustawień.
Zakres Y będzie obejmował naszą zmienną zależną, PKB. Natomiast w Zakresie X wybierzemy wszystkie kolumny zmiennej X. Proszę zauważyć, że jest to taka sama procedura, jak w przypadku pojedynczej regresji liniowej, z tą różnicą, że wybieramy wiele kolumn dla Zakresu X.
Pamiętaj, że Excel wymaga, aby wszystkie zmienne X znajdowały się w sąsiednich kolumnach.
Jak wybrałem kolumnę Tytuły, ważne jest, aby zaznaczyć pole wyboru Etykiety. 95% przedział ufności jest odpowiedni w większości scenariuszy analizy finansowej, więc nie będziemy tego zmieniać.
Możesz następnie rozważyć umieszczenie danych w tym samym arkuszu lub w nowym. Nowy arkusz zwykle działa najlepiej, ponieważ narzędzie wstawia dość dużo danych.
Zaznaczę również wszystkie dodatkowe opcje na dole. Rzadko kiedy korzystam z nich wszystkich, ale łatwiej jest usunąć te, które nie są nam potrzebne, niż ponownie uruchamiać całość.
Dołącz do naszego Newslettera aby otrzymać DARMOWY szablon analizy porównawczej w Excelu
Ocena wyników regresji
Teraz, gdy mamy już podsumowanie wyników z Excela, zbadajmy nasz model regresji.
Informacje, które uzyskaliśmy z modułu analizy danych programu Excel, zaczynają się od statystyk regresji.
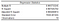
R kwadrat jest najważniejszą z nich, więc możemy zacząć od jego sprawdzenia. Konkretnie, w naszym przypadku powinniśmy spojrzeć na Skorygowany kwadrat R, ponieważ mamy więcej niż jedną zmienną X. Daje nam to pogląd na ogólną dobroć dopasowania.
Korygowany kwadrat R równy 0,98 oznacza, że nasz model regresji może wyjaśnić około 98% zmienności zmiennej zależnej Y (PKB) wokół średniej wartości obserwacji (średnia z naszej próby). Innymi słowy, 98% zmienności w ŷ (y-hat, nasza zmienna zależna przewidywania) jest przechwytywane przez nasz model. Tak wysoka wartość zwykle wskazywałaby na to, że z naszym modelem może być jakiś problem. Będziemy kontynuować nasz model, ale zbyt wysokie R Squared może być problematyczne w prawdziwym scenariuszu życia. Proponuję przeczytać ten artykuł na Statistics by Jim, aby dowiedzieć się, dlaczego zbyt dobre nie zawsze jest właściwe w odniesieniu do R kwadrat.
Błąd standardowy daje nam szacunek standardowego odchylenia błędu (reszt). Ogólnie rzecz biorąc, jeśli współczynnik jest duży w porównaniu do błędu standardowego, prawdopodobnie jest statystycznie istotny.
Analiza wariancji (ANOVA)

Sekcja Analiza wariancji jest czymś, co często pomijamy podczas modelowania Regresji. Jednak może ona dostarczyć cennych spostrzeżeń i warto się jej przyjrzeć. Więcej o przeprowadzaniu testu ANOVA i przykładowy model można przeczytać w naszym dedykowanym artykule.
Ta tabela daje nam ogólny test istotności parametrów regresji.
Kolumna F tabeli ANOVA daje nam ogólny test F hipotezy zerowej, że wszystkie współczynniki są równe zero. Hipotezą alternatywną jest to, że przynajmniej jeden ze współczynników nie jest równy zeru. Kolumna Significance F pokazuje nam wartość p dla testu F. Ponieważ jest ona niższa od poziomu istotności 0,05 (przy wybranym przez nas poziomie ufności 95%), możemy odrzucić hipotezę zerową, że wszystkie współczynniki są równe zero. Oznacza to, że nasze parametry regresji nie są wspólnie nieistotne statystycznie.
Więcej na temat testowania hipotez można przeczytać w naszym dedykowanym artykule.
Kolejna tabela dostarcza nam informacji na temat współczynników w naszym modelu regresji wielorakiej i jest najbardziej ekscytującą częścią analizy.

Mamy tutaj wiele szczegółów dla punktu przecięcia i każdego z naszych predyktorów (zmiennych niezależnych). Zbadajmy, co te kolumny reprezentują:
- Współczynniki – są to oszacowania uzyskane metodą najmniejszych kwadratów;
- Błąd standardowy – odchylenie standardowe oszacowań metodą najmniejszych kwadratów;
- T-Stat – jest to statystyka t dla hipotezy zerowej, że współczynnik jest równy zero, versus hipoteza alternatywna, że jest różny od zera;
- Wartość P dla testu t;
- Dolne i górne 95% określają przedział ufności dla współczynników.
Test Istotności Statystycznej
Jest to test hipotezy zerowej mówiącej, że współczynnik ma nachylenie równe zero. Możemy przyjrzeć się wartościom p dla każdego współczynnika i porównać je z poziomem istotności 0,05.
Jeśli nasza wartość p jest mniejsza niż poziom istotności, oznacza to, że nasza zmienna niezależna jest statystycznie istotna dla modelu. Patrząc na nasze predyktory od X1 do X3, zauważamy, że tylko X3 Employee Compensation ma p-value poniżej 0.05, co oznacza, że X1 Education Spend i X2 Unemployment Rate nie wydają się być statystycznie istotne dla naszego modelu regresji.
Ponieważ nie możemy odrzucić hipotezy zerowej (że współczynniki są równe zero), możemy wyeliminować X1 i X2 z modelu. Możemy to również potwierdzić, ponieważ wartość zero leży pomiędzy dolnym i górnym przedziałem ufności.
Możemy zdecydować się na uruchomienie modelu bez zmiennych X1 i X2 i ocenić, czy spowoduje to znaczący spadek skorygowanej miary R kwadrat. Jeśli tak nie jest, to można bezpiecznie usunąć X1 i X2 z modelu regresji.
Jeśli to zrobimy, otrzymamy następujące statystyki regresji.

Widzimy brak spadku R kw, więc możemy bezpiecznie usunąć X1 i X2 z naszego modelu i uprościć go do pojedynczej regresji liniowej.
Wyjście resztowe
Rezydukty informują o tym, jak bardzo rzeczywiste punkty danych (y) odbiegają od przewidywanych punktów danych (ŷ), bazując na naszym modelu regresji.

Wyjście prawdopodobieństwa
Ta tabela pokazuje zaobserwowane wartości zmiennej niezależnej (y) i odpowiadające im percentyle próby. Pierwszy percentyl można obliczyć jako (100 / 2 * liczba obserwacji), a kolejne jako poprzedni percentyl + (100 / 2).

Wykresy reszt
Analiza regresji wielorakiej daje nam jeden wykres dla każdej zmiennej niezależnej w stosunku do reszt. Możemy użyć tych wykresów, aby ocenić, czy nasze przykładowe dane pasują do założeń wariancji dotyczących liniowości i jednorodności.
Jednorodność oznacza, że wykres powinien wykazywać losowy wzór i mieć stałą pionową rozpiętość.
Liniowość wymaga, aby reszty miały średnią równą zero. Możemy to zaobserwować wizualnie, oceniając, czy punkty są rozłożone mniej więcej równo poniżej i powyżej osi x.



Ploty dopasowania liniowego
Model dostarcza nam jeden wykres dopasowania liniowego dla każdej zmiennej niezależnej (predyktora). Pokazuje on przewidywane wartości (ŷ) w stosunku do obserwowanych wartości (y). Im bardziej się one pokrywają, tym lepiej nasz model przewiduje zmienną zależną na podstawie regresorów.



Normalny wykres prawdopodobieństwa
Normalny wykres prawdopodobieństwa pomaga nam określić, czy dane pasują do rozkładu normalnego. Możemy dodać linię trendu i ocenić, czy punkty danych są zgodne z linią prostą. W naszym przypadku jest to dość oczywiste i możemy nawet nie dodawać linii trendu.

Przykładowy model w Excelu można pobrać w oryginalnym artykule.
Ograniczenia Excela
Jako że Excel nie jest specjalistycznym oprogramowaniem statystycznym, istnieją pewne nieodłączne ograniczenia podczas uruchamiania modelu regresji, których powinniśmy być świadomi:
- Kolumny dla wszystkich regresorów (zmiennych niezależnych) muszą ze sobą sąsiadować;
- Możemy mieć do 16 predyktorów (nie pamiętam, gdzie to przeczytałem, więc traktuj to z ostrożnością);
- Analiza regresji w Excelu zakłada, że błędy są niezależne i mają stałą wariancję (homoskedastyczność);
- Jeśli pójdziemy drogą funkcji, ważne jest, aby wiedzieć, że funkcje Excela SLOPE, INTERCEPT i FORECAST nie działają dla regresji wielorakiej. Natomiast TREND i LINEST działają tak samo, jak w przypadku pojedynczego modelu regresji, ale przyjmują wartości dla wielu zmiennych X.
Wnioski
Zaczęliśmy od trzech zmiennych niezależnych, przeprowadziliśmy analizę regresji i stwierdziliśmy, że dwa predyktory nie mają znaczenia statystycznego dla naszego modelu.
Wyeliminowaliśmy je, aby otrzymać model pojedynczej regresji liniowej.
Jak już będziesz zadowolony ze swojego modelu, możesz zbudować równanie regresji, tak jak to omówiliśmy w innych artykułach. Dzięki temu równaniu możesz prognozować zmienną zależną na przyszłość.
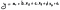
Gdzie:
- y jest naszą zmienną zależną;
- a jest przechwytem (naszą stałą) ze statystyki regresji;
- b, c, i d są współczynnikami dla każdej zmiennej;
- x1 do x3 są zmiennymi niezależnymi (naszymi regresorami lub predyktorami);
- ɛ jest błędem lub resztami, które często możemy wykluczyć.
Pamiętajmy, że ten artykuł ma na celu zilustrowanie koncepcji przeprowadzania analizy regresji wielorakiej w Excelu. Stara się on wyjaśnić, na czym powinniśmy się skupić podczas oceny wyników. Każdy dobry model zaczyna się od ustalenia rozsądnych założeń i oczekiwań, w czym nie jestem ekspertem, więc nie twierdzę, że wybrane zmienne zależne i niezależne były właściwym wyborem.
Dziękuję za przeczytanie! Możesz okazać swoje wsparcie, dzieląc się tym artykułem z kolegami i przyjaciółmi.