Control Tutorials for MATLAB and Simulink - Introduction: PID Controller Design

W tym tutorialu przedstawimy prostą, ale uniwersalną strukturę kompensatora sprzężenia zwrotnego: regulator proporcjonalno-całkująco-różniczkujący (PID). Regulator PID jest powszechnie stosowany, ponieważ jest bardzo zrozumiały i dość skuteczny. Jedną z zalet regulatora PID jest to, że wszyscy inżynierowie rozumieją koncepcję różnicowania i całkowania, więc mogą zaimplementować system sterowania nawet bez dogłębnego zrozumienia teorii sterowania. Ponadto, mimo że kompensator jest prosty, jest on dość wyrafinowany w tym sensie, że ujmuje historię systemu (poprzez integrację) i przewiduje przyszłe zachowanie systemu (poprzez różnicowanie). Omówimy wpływ każdego z parametrów PID na dynamikę systemu z zamkniętą pętlą i zademonstrujemy, jak wykorzystać regulator PID do poprawy działania systemu.

Kluczowe polecenia MATLAB użyte w tym tutorialu to: tf , step , pid , feedback , pidtune

PID Overview

W tym tutorialu rozważymy następujący system z jednolitym sprzężeniem zwrotnym:

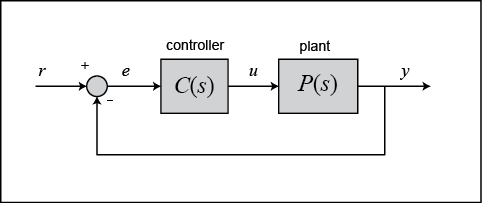
Wyjście regulatora PID, które jest równe wejściu sterującemu do instalacji, jest obliczane w dziedzinie czasu z błędu sprzężenia zwrotnego w następujący sposób:

(1) $u(t) = K_p e(t) + K_i \int e(t)dt + K_p \frac{de}{dt}$

Pierw przyjrzyjmy się, jak działa regulator PID w układzie zamkniętym, korzystając ze schematu przedstawionego powyżej. Zmienna ( $e$ ) reprezentuje błąd śledzenia, czyli różnicę między wyjściem pożądanym ( $r$ ) a wyjściem rzeczywistym ( $y$ ). Ten sygnał błędu ( $e$ ) jest podawany do regulatora PID, a regulator oblicza zarówno pochodną, jak i całkę tego sygnału błędu w odniesieniu do czasu. Sygnał sterujący ( $u$ ) do instalacji jest równy wzmocnieniu proporcjonalnemu ( $K_p$ ) pomnożonemu przez wielkość błędu plus wzmocnienie całkowe ( $u$ ). wzmocnienie całkowe ( $K_i$ ) razy całka błędu plus wzmocnienie pochodnej ( $K_d$ ) razy pochodna błędu.

Ten sygnał sterujący ( $u$ ) jest podawany do zakładu i uzyskuje się nowe wyjście ( $y$ ). Nowy sygnał wyjściowy ( $y$ ) jest następnie podawany z powrotem i porównywany z referencyjnym, aby znaleźć nowy sygnał błędu ( $e$ ). Sterownik bierze ten nowy sygnał błędu i oblicza aktualizację wejścia sterującego. Proces ten trwa przez cały czas działania sterownika.

Funkcję przenoszenia regulatora PID można znaleźć poprzez transformację Laplace’a równania (1).

(2) $K_p + \frac {K_i} {s} + K_d s = \frac{K_d s^2 + K_p s + K_i} {s}$

gdzie $K_p$ = wzmocnienie proporcjonalne, $K_i$ = wzmocnienie całkowe, a $K_d$ = wzmocnienie pochodne.

Możemy zdefiniować regulator PID w MATLABie używając bezpośrednio modelu funkcji przenoszenia, na przykład:

Kp = 1;Ki = 1;Kd = 1;s = tf('s');C = Kp + Ki/s + Kd*s

C = s^2 + s + 1 ----------- s Continuous-time transfer function.

Alternatywnie, możemy użyć obiektu pid MATLABa do wygenerowania równoważnego regulatora czasu ciągłego w następujący sposób:

C = pid(Kp,Ki,Kd)

C = 1 Kp + Ki * --- + Kd * s s with Kp = 1, Ki = 1, Kd = 1 Continuous-time PID controller in parallel form.

Przekształćmy obiekt pid na funkcję transferu, aby sprawdzić, czy daje on taki sam wynik jak powyżej:

tf(C)

ans = s^2 + s + 1 ----------- s Continuous-time transfer function.

Charakterystyka członów P, I, i D

Zwiększenie wzmocnienia proporcjonalnego ( $K_p$ ) skutkuje proporcjonalnym zwiększeniem sygnału sterującego dla tego samego poziomu błędu. Fakt, że sterownik będzie „naciskał” mocniej dla danego poziomu błędu powoduje, że układ zamknięty reaguje szybciej, ale również bardziej się przesterowuje. Innym efektem zwiększania $K_p$ jest tendencja do zmniejszania, ale nie eliminowania, błędu stanu ustalonego.

Dodanie członu pochodnego do regulatora ( $K_d$ ) dodaje zdolność regulatora do „przewidywania” błędu. W przypadku prostego sterowania proporcjonalnego, jeśli $K_p$ jest stałe, jedynym sposobem zwiększenia sterowania jest wzrost błędu. W przypadku sterowania pochodną sygnał sterujący może stać się duży, jeśli błąd zaczyna wzrastać, nawet gdy wielkość błędu jest jeszcze stosunkowo mała. To oczekiwanie ma tendencję do dodawania tłumienia do systemu, zmniejszając w ten sposób przekroczenie zakresu. Dodanie terminu pochodnej nie ma jednak wpływu na błąd stanu ustalonego.

Dodanie członu całkującego do regulatora ( $K_i$ ) ma tendencję do zmniejszania błędu stanu ustalonego. Jeśli występuje trwały, stały błąd, całka buduje i buduje, zwiększając w ten sposób sygnał sterujący i obniżając błąd. Wadą całki jest jednak to, że może ona uczynić system bardziej powolnym (i oscylacyjnym), ponieważ kiedy sygnał błędu zmienia znak, może zająć chwilę, aby integrator się „rozwinął”.

Ogólny wpływ każdego parametru regulatora ( $K_p$ $K_d$ $K_i$ ) na system z zamkniętą pętlą jest podsumowany w poniższej tabeli. Uwaga, te wytyczne obowiązują w wielu przypadkach, ale nie we wszystkich. Jeśli naprawdę chcesz poznać efekt dostrajania poszczególnych wzmocnień, będziesz musiał wykonać więcej analiz lub przeprowadzić testy na rzeczywistym systemie.

CL RESPONSE	RISE TIME	OVERSHOOT	SETTLING TIME	S-S ERROR
Kp	Zmniejszyć	Wzrost	Mała zmiana	Zmniejszenie
Ki	Zmniejszenie	Zwiększenie	Wzrost	Zmniejszenie
Kd	Mała zmiana	Zmniejszenie	Zmniejszenie	Bez zmian

Przykładowy problem

Załóżmy, że mamy prosty układ masa- sprężyna- amortyzator.układ sprężyna-tłumik.

Równanie rządzące tym układem ma postać

(3) $m\dot{x} + bdot{x} + kx = F$

Przykładając transformatę Laplace’a do równania rządzącego, otrzymujemy

(4) $ms^{2}X(s) + bsX(s) + kX(s) = F(s)$

Funkcja transferu pomiędzy siłą wejściową $F(s)$ a przemieszczeniem wyjściowym $X(s)$ staje się wtedy

(5) $\frac{X(s)}{F(s)} = \frac{1}{ms^2 + bs + k}$

Let

 m = 1 kg b = 10 N s/m k = 20 N/m F = 1 N

Podstawiając te wartości do powyższej funkcji transferu

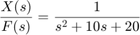
(6) $\frac{X(s)}{F(s)} = \frac{1}{s^2 + 10s + 20}$

Celem tego zadania jest pokazanie, jak każdy z członów, $K_p$ $K_i$ , oraz $K_d$ , przyczynia się do uzyskania wspólnych celów:

Szybki czas narastania
Minimalne przekroczenia
Zerowy błąd stanu ustalonego

Open-Loop Step Response

Pierw przyjrzyjmy się odpowiedzi skokowej w pętli otwartej. Utwórz nowy plik m i uruchom następujący kod:

s = tf('s');P = 1/(s^2 + 10*s + 20);step(P)

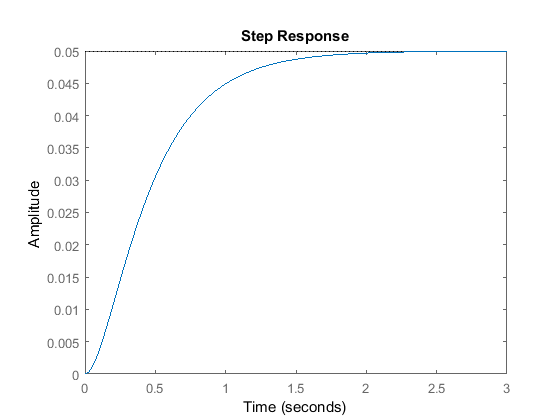
Wzmocnienie DC funkcji przenoszenia instalacji wynosi 1/20, więc 0,05 jest końcową wartością wyjścia na jednostkowy krok wejściowy. Odpowiada to błędowi stanu ustalonego 0,95, który jest dość duży. Ponadto, czas narastania wynosi około jednej sekundy, a czas ustalania się wynosi około 1,5 sekundy. Zaprojektujmy regulator, który zmniejszy czas narastania, zmniejszy czas ustalania i wyeliminuje błąd stanu ustalonego.

Sterownik proporcjonalny

Z tabeli przedstawionej powyżej widzimy, że sterownik proporcjonalny ( $K_p$ ) zmniejsza czas narastania, zwiększa przekroczenie i zmniejsza błąd stanu ustalonego.

Funkcja przeniesienia w pętli zamkniętej naszego systemu z jednostronnym sprzężeniem zwrotnym i regulatorem proporcjonalnym ma następującą postać, gdzie $X(s)$ jest naszym wyjściem (równa się $Y(s)$ ), a nasze odniesienie $R(s)$ jest wejściem:

(7) $T(s) = \frac{X(s)}{R(s)} = \frac{K_p}{s^2 + 10s + (20 + K_p)}$

Pozwólmy, aby wzmocnienie proporcjonalne ( $K_p$ ) było równe 300 i zmieńmy plik m-.na następujący:

Kp = 300;C = pid(Kp)T = feedback(C*P,1)t = 0:0.01:2;step(T,t)

C = Kp = 300 P-only controller.T = 300 ---------------- s^2 + 10 s + 320 Continuous-time transfer function.

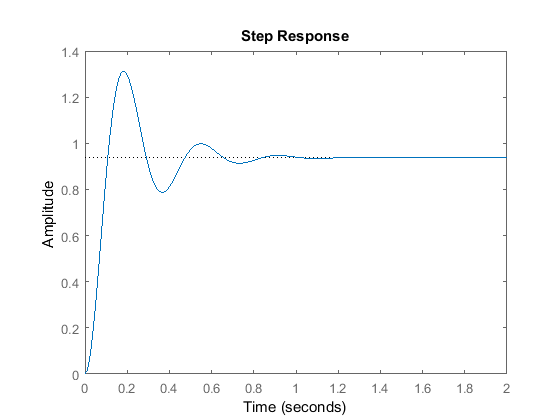
Powyższy wykres pokazuje, że regulator proporcjonalny zmniejszył zarówno czas narastania, jak i błąd stanu ustalonego, zwiększył przekroczenie oraz zmniejszył czas ustalania o niewielką wartość.

Regulator proporcjonalno-dodatkowy

Przyjrzyjrzyjmy się teraz regulatorowi PD. Z tabeli powyżej widzimy, że dodanie sterowania pochodną ( $K_d$ ) ma tendencję do zmniejszania zarówno przerostu jak i czasu ustalania. Funkcja przenoszenia w pętli zamkniętej danego układu z regulatorem PD wynosi:

(8) $T(s) = \frac{X(s)}{R(s)} = \frac{K_d s + K_p}{s^2 + (10 + K_d) s + (20 + K_p)}$

Niech $K_p$ będzie równy 300 jak poprzednio i niech $K_d$ będzie równy 10. Wpisz poniższe polecenia do pliku m i uruchom go w oknie poleceń MATLABa.

Kp = 300;Kd = 10;C = pid(Kp,0,Kd)T = feedback(C*P,1)t = 0:0.01:2;step(T,t)

C = Kp + Kd * s with Kp = 300, Kd = 10 Continuous-time PD controller in parallel form.T = 10 s + 300 ---------------- s^2 + 20 s + 320 Continuous-time transfer function.

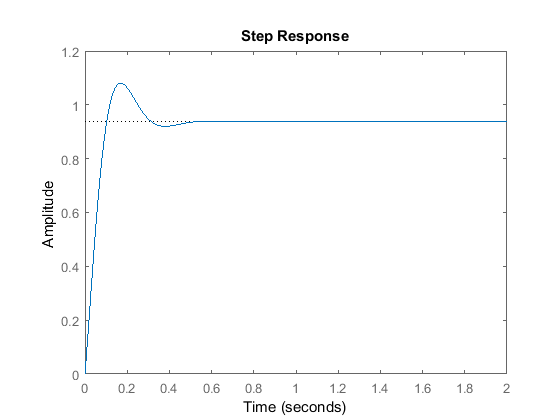
Ten wykres pokazuje, że dodanie członu pochodnej zmniejszyło zarówno przerost, jak i czas ustalania, a miało pomijalny wpływ na czas narastania i błąd stanu ustalonego.

Sterowanie proporcjonalno-całkująco-różniczkujące

Przed przejściem do sterowania PID, zbadajmy sterowanie PI. Z tabeli widzimy, że dodanie sterowania całkowego ( $K_i$ ) ma tendencję do zmniejszania czasu narastania, zwiększania zarówno przerostu jak i czasu ustalania oraz zmniejszania błędu stanu ustalonego. Dla podanego układu, funkcja transferu w pętli zamkniętej z regulatorem PI wynosi:

(9) $T(s) = \frac{X(s)}{R(s)} = \frac{K_p s + K_i}{s^3 + 10 s^2 + (20 + K_p )s + K_i}$

Zmniejszmy $K_p$ do 30, i niech $K_i$ będzie równy 70. Utwórz nowy plik m i wprowadź następujące komendy.

Kp = 30;Ki = 70;C = pid(Kp,Ki)T = feedback(C*P,1)t = 0:0.01:2;step(T,t)

C = 1 Kp + Ki * --- s with Kp = 30, Ki = 70 Continuous-time PI controller in parallel form.T = 30 s + 70 ------------------------ s^3 + 10 s^2 + 50 s + 70 Continuous-time transfer function.

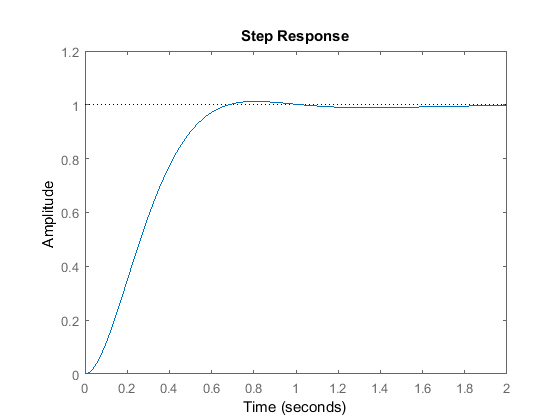
Uruchom ten m-plik w oknie poleceń MATLABa i powinieneś wygenerować powyższy wykres. Zmniejszyliśmy wzmocnienie proporcjonalne ( $K_p$ ), ponieważ regulator całkujący również skraca czas narastania i zwiększa przekroczenie, tak jak regulator proporcjonalny (efekt podwójny). Powyższa odpowiedź pokazuje, że regulator całkujący wyeliminował błąd stanu ustalonego w tym przypadku.

Kontrola proporcjonalno-całkująco-różniczkująca

Przeanalizujmy teraz kontrolę PID. Funkcja transferu w pętli zamkniętej danego układu z regulatorem PID wynosi:

(10) $T(s) = \frac{X(s)}{R(s)} = \frac{K_d s^2 + K_p s + K_i}{s^3 + (10 + K_d)s^2 + (20 + K_p)s + K_i }$

Po kilku iteracjach dostrajania, wzmocnienia $K_p$ $K_i$ = 300, oraz $K_d$ = 50 zapewniły pożądaną odpowiedź. Aby potwierdzić, wprowadź następujące polecenia do pliku m i uruchom go w oknie poleceń. Powinieneś uzyskać następującą odpowiedź kroku.

Kp = 350;Ki = 300;Kd = 50;C = pid(Kp,Ki,Kd)T = feedback(C*P,1);t = 0:0.01:2;step(T,t)

C = 1 Kp + Ki * --- + Kd * s s with Kp = 350, Ki = 300, Kd = 50 Continuous-time PID controller in parallel form.

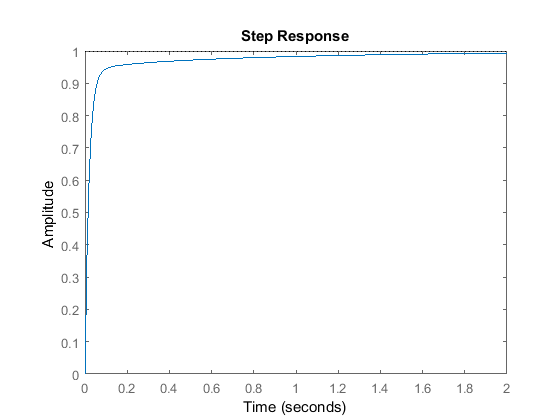
Teraz zaprojektowaliśmy system z zamkniętą pętlą bez przeregulowania, z szybkim czasem narastania i bez błędu w stanie ustalonym.

Ogólne wskazówki dotyczące projektowania regulatora PID

Przy projektowaniu regulatora PID dla danego systemu, należy postępować zgodnie z krokami przedstawionymi poniżej, aby uzyskać pożądaną odpowiedź.

Uzyskać odpowiedź w pętli otwartej i określić, co należy poprawić
Dodać sterowanie proporcjonalne w celu poprawy czasu narastania
Dodać sterowanie pochodne w celu redukcji przekroczenia
Dodać sterowanie całkujące w celu redukcji błędu stanu ustalonego
Dodać sterowanie całkujące w celu redukcji błędustanu
Dostosuj każde z wzmocnień , i aż do uzyskania pożądanej odpowiedzi ogólnej. Zawsze można odwołać się do tabeli pokazanej na tej stronie „PID Tutorial”, aby dowiedzieć się, który sterownik kontroluje jaką charakterystykę.

Na koniec, proszę pamiętać, że nie trzeba implementować wszystkich trzech regulatorów (proporcjonalnego, pochodnej i całki) w jednym systemie, jeśli nie jest to konieczne. Na przykład, jeśli kontroler PI spełnia dane wymagania (jak w powyższym przykładzie), to nie musisz implementować kontrolera pochodnej w systemie. Utrzymuj sterownik tak prosty jak to tylko możliwe.

Przykład strojenia kontrolera PI na rzeczywistym systemie fizycznym można znaleźć pod poniższym linkiem. Ten przykład również zaczyna ilustrować niektóre wyzwania związane z implementacją sterowania, w tym: nasycenie sterowania, zwijanie integratora i wzmocnienie szumu.

Automatyczne dostrajanie PID

MATLAB dostarcza narzędzi do automatycznego wyboru optymalnych wzmocnień PID, co czyni opisany powyżej proces prób i błędów zbędnym. Możesz uzyskać dostęp do algorytmu strojenia bezpośrednio używając pidtune lub poprzez ładny graficzny interfejs użytkownika (GUI) używając pidTuner.

Automatyczny algorytm dostrajania MATLABa wybiera wzmocnienia PID w celu zrównoważenia wydajności (czas odpowiedzi, szerokość pasma) i odporności (marginesy stabilności). Domyślnie, algorytm projektuje dla 60-stopniowego marginesu fazy.

Poznajmy te zautomatyzowane narzędzia, generując najpierw regulator proporcjonalny dla układu masa-sprężyna-tłumik, wpisując polecenie pokazane poniżej. W przedstawionej składni, P jest wcześniej wygenerowanym modelem instalacji, a 'p' określa, że tuner ma zastosować regulator proporcjonalny.

 pidTuner(P,'p')

Powinno pojawić się okno GUI programu pidTuner, jak pokazano poniżej.

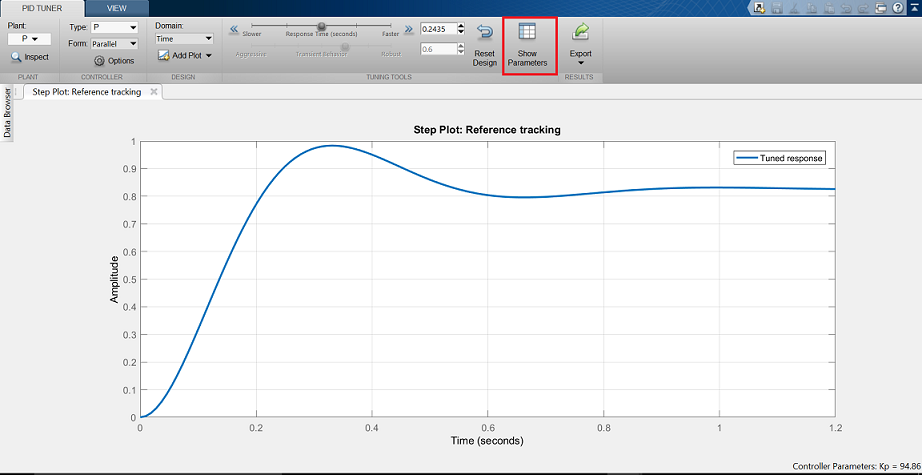
Zauważ, że pokazana odpowiedź skokowa jest wolniejsza niż w przypadku sterownika proporcjonalnego, który zaprojektowaliśmy ręcznie. Kliknij teraz na przycisk Show Parameters w prawym górnym rogu. Zgodnie z oczekiwaniami, wzmocnienie proporcjonalne, $K_p$ , jest mniejsze niż to, które zastosowaliśmy, $K_p$ < 300.

Możemy teraz interaktywnie dostroić parametry kontrolera i natychmiast zobaczyć wynikową odpowiedź w oknie GUI. Spróbuj przeciągnąć suwak Response Time w prawo do wartości 0,14 s, jak pokazano na poniższym rysunku. Powoduje to, że odpowiedź rzeczywiście przyspiesza i możemy zobaczyć, że $K_p$ jest teraz bliższy ręcznie wybranej wartości. Możemy również zobaczyć inne parametry wydajności i odporności systemu. Zauważ, że zanim wyregulowaliśmy suwak, docelowy margines fazy wynosił 60 stopni. Jest to wartość domyślna dla pidTunera i generalnie zapewnia dobrą równowagę między odpornością a wydajnością.

Spróbujmy teraz zaprojektować regulator PID dla naszego systemu. Podając jako drugi parametr wcześniej zaprojektowany lub (bazowy) regulator, C, pidTuner zaprojektuje inny regulator PID (zamiast P lub PI) i porówna odpowiedź układu z automatycznym regulatorem z odpowiedzią z regulatora bazowego.

 pidTuner(P,C)

W oknie wyjściowym widzimy, że automatyczny sterownik reaguje wolniej i wykazuje więcej przeregulowań niż linia bazowa. Wybierz teraz opcję Domain: Frequency z paska narzędzi, co ujawnia parametry strojenia w dziedzinie częstotliwości.

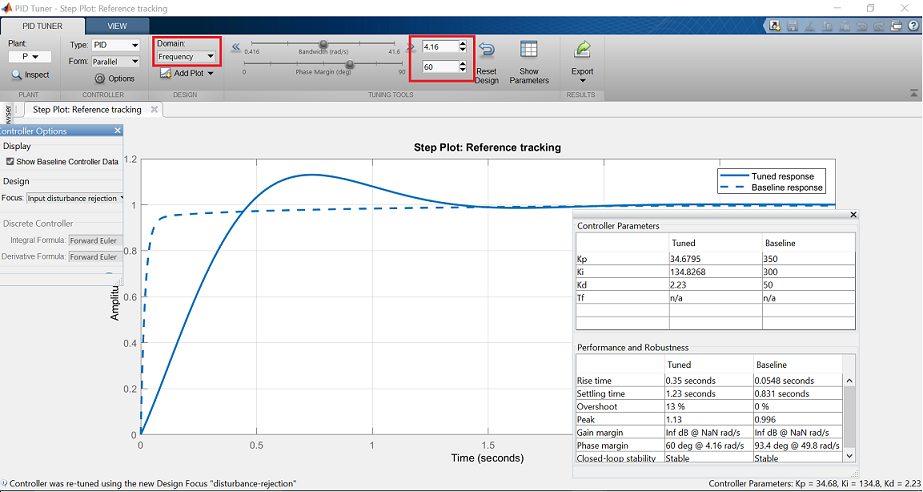
Teraz wpisz 32 rad/s dla Bandwidth i 90 deg dla Phase Margin, aby wygenerować sterownik o wydajności zbliżonej do linii podstawowej. Należy pamiętać, że większa szerokość pasma zamkniętej pętli skutkuje szybszym czasem narastania, a większy margines fazy zmniejsza przekroczenie i poprawia stabilność systemu.

Na koniec zauważmy, że możemy wygenerować ten sam kontroler używając narzędzia wiersza poleceń pidtune zamiast GUI pidTunera, stosując następującą składnię.

opts = pidtuneOptions('CrossoverFrequency',32,'PhaseMargin',90); = pidtune(P, 'pid', opts)

C = 1 Kp + Ki * --- + Kd * s s with Kp = 320, Ki = 796, Kd = 32.2 Continuous-time PID controller in parallel form.info = struct with fields: Stable: 1 CrossoverFrequency: 32 PhaseMargin: 90

Opublikowano w MATLAB® 9.2

Guinguette Marais Poitevin

Blog

Wprowadzenie: PID Controller Design