Diese Frage ist komplizierter, als Sie vielleicht denken

Wie viele Ameisen braucht es, um die Erde anzuheben? Dies mag wie eine sehr einfache Frage erscheinen. Im Grunde müssten wir zwei Dinge wissen: 1, wie viel Masse eine Ameise heben kann, und 2, wie viel Masse die Erde hat. Dividieren Sie die zweite Zahl durch die erste und Sie erhalten die gewünschte Antwort. Richtig?
Nun, zunächst einmal müssen wir entscheiden, wo wir die Erde in unserem kleinen Gedankenexperiment anheben wollen. Wenn wir Fragen der Art „Wie viel X braucht man, um Y zu heben?“ stellen, meinen wir normalerweise „auf der Erde“. Dazu müssen wir die Erde auf der Erde anheben, aber da dies ein Gedankenexperiment ist, lassen wir uns davon nicht beirren. Nehmen wir an, wir sind auf der Erde und haben eine „zweite Erde“, E2, die wir mit unseren Ameisen anheben wollen. Alles, was an E2 wichtig ist, ist, dass sie die gleiche Masse, Form und Größe wie unsere Erde hat.
E2 hat ein Gravitationsfeld, das dem der Erde entspricht.
Okay, also können wir jetzt einfach die Masse von E2 durch die Masse, die eine Ameise heben kann, teilen, wie wir gesagt haben, richtig? Nicht ganz. Die Frage ist etwas komplizierter als das. Sehen Sie, diese Methode funktioniert für „normale“ Objekte, wie ein Buch, einen Stein oder sogar einen Bus. E2 jedoch ist viel schwerer als diese. So viel, dass es ein Gravitationsfeld hat, das dem der Erde entspricht (da seine Masse gleich der der Erde ist). Bei normalen fallenden Objekten müssen wir nur das Gravitationsfeld der Erde berücksichtigen, nicht das des Objekts, das praktisch nicht vorhanden ist. In einer solchen Situation können wir die Kraft, die die Erde auf ein Objekt ausübt, leicht berechnen, indem wir die Masse des Objekts in Kilogramm mit 9,81 multiplizieren, um eine Kraft in Newton zu erhalten. E2 ist dafür jedoch zu schwer.
Was wir wissen müssen, ist die Kraft, die unser hypothetisches E2 gegen die Erde hält.
Was wir wissen müssen, ist die Kraft, die unser hypothetisches E2 gegen die Erde hält. Wir können dann berechnen, wie viele Ameisen nötig sind, um dieser Kraft entgegenzuwirken. Die Kraft, die E2 am Boden hält, kann mit der folgenden Formel berechnet werden, indem man die Kraft F zwischen zwei Massen (beide mit m bezeichnet) mit einem Abstand r zwischen ihnen berechnet:
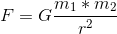
G ist die Gravitationskonstante. Wenn E2 auf der Erde „sitzt“, sind die Zentren der beiden Massen 12742000 Meter voneinander entfernt (der zweifache Erdradius). Setzt man die restlichen Zahlen in die Formel ein, erhält man eine Kraft von 1,4662378 * 10²⁵ Newton. Interessanterweise ist diese Zahl ein paar Mal NIEDRIGER, als wenn wir die Kraft (fälschlicherweise) so berechnen würden, wie wir es für „normale“ Objekte tun, die auf die Erde fallen (Multiplikation mit 9,81). Obwohl wir einen zusätzlichen Gravitationskörper mit eigener Kraft im Spiel haben, ist die resultierende Kraft geringer. Wie ist das möglich? Die Antwort ist die Entfernung. Je weiter man sich von der Erde entfernt, desto geringer ist die Gravitationskraft, und das Zentrum von E2 ist 6371 Kilometer von der Erdoberfläche entfernt.
Es gibt genug Ameisen, um jeden Menschen zu tragen.
Also, zurück zu unserer ursprünglichen Frage. Wir müssen immer noch wissen, wie viel Hebekraft eine Ameise aufbringen kann. Ich finde sehr unterschiedliche Zahlen darüber, wie viel eine Ameise heben kann, aber ich werde die Zahl des 50-fachen ihres eigenen Körpergewichts verwenden. Kombinieren Sie dies mit einem Ameisengewicht von, sagen wir, 2 Milligramm. Das 50-fache ihrer Masse wäre 100 Milligramm, was eine Hubkraft von 0,000981 Newton ergibt. Wir brauchen 1,4662378 * 10²⁵ Newton, also etwa 1,49 * 10²⁸ Ameisen! Nun, die Gesamtmenge der Ameisen auf diesem Planeten wurde auf 10¹⁶ geschätzt, also haben wir nicht annähernd genug Ameisen, um unseren Planeten anzuheben. Interessanterweise haben wir angesichts unserer Anzahl genug, um alle Menschen zu tragen. 10¹⁶ Ameisen und 7,73 * 10⁹ Menschen, wir haben mehr als eine Million Ameisen für jeden Menschen. Eine Million Ameisen zu je 2 Milligramm haben eine Gesamtmasse von 2 kg. Da sie das 50-fache ihrer Körpermasse tragen können, ergibt das 100 Kilogramm. Der durchschnittliche Mensch ist viel leichter als das!