Questa domanda è più complicata di quanto si possa pensare

Quante formiche servono per sollevare la Terra? Questa può sembrare una domanda molto semplice. Fondamentalmente, avremmo bisogno di sapere due cose: 1, quanta massa può sollevare una formica e 2, quanta massa ha la Terra. Dividendo il secondo numero per il primo si ottiene la risposta desiderata. Giusto?
Bene, prima di tutto, dobbiamo decidere dove vogliamo sollevare la Terra nel nostro piccolo esperimento mentale. Di solito quando facciamo domande del tipo “Quanto X ci vuole per sollevare Y”, intendiamo “sulla Terra”. Per questo dobbiamo sollevare la Terra sulla Terra, ma dato che questo è un esperimento di pensiero, non lasciamo che questo ci intralci. Supponiamo di essere sulla Terra e di avere una “seconda Terra”, E2, che vogliamo che le nostre formiche sollevino. Tutto ciò che è importante di E2 è che ha la stessa massa, forma e dimensione della nostra Terra.
E2 ha un campo gravitazionale uguale a quello della Terra.
Ok, quindi ora possiamo semplicemente dividere la massa di E2 per quanta massa una formica può sollevare, come abbiamo detto, giusto? Non proprio. La questione è un po’ più complicata di così. Vedete, questo metodo funziona per oggetti “normali”, come un libro, una roccia, o anche un autobus. E2, invece, è molto più pesante di questo. Tanto che ha un campo gravitazionale uguale a quello della Terra (poiché la sua massa è uguale a quella della Terra). Per gli oggetti normali che cadono, dobbiamo tenere conto solo del campo gravitazionale della Terra, non di quello dell’oggetto, che è effettivamente inesistente. In tale situazione, possiamo facilmente calcolare la forza che la Terra ha su un oggetto moltiplicando la massa in chilogrammi dell’oggetto con 9,81 per ottenere una forza in Newton. E2, tuttavia, è troppo pesante per questo.
Quello che dobbiamo sapere è la forza che tiene il nostro ipotetico E2 contro la Terra.
Quello che dobbiamo sapere è la forza che tiene il nostro ipotetico E2 contro la Terra. Possiamo poi calcolare quante formiche ci vogliono per contrastare questa forza. La forza che tiene giù E2 può essere calcolata con la seguente formula, calcolando la forza F tra due masse (entrambe indicate con una m) con una distanza r tra loro:
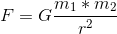
G è la costante gravitazionale. Se E2 si “siede” sulla Terra, i centri delle due masse sono distanti 12742000 metri (due volte il raggio della Terra). Riempiendo il resto dei numeri della formula si ottiene una forza di 1,4662378 * 10²⁵ Newton. È interessante notare che questo numero è un po’ più basso di quello che sarebbe stato se avessimo (erroneamente) calcolato la forza come facciamo per gli oggetti “normali” che cadono verso la Terra (moltiplicando per 9,81). Anche se abbiamo un corpo gravitazionale in più con la sua forza nel gioco, la forza risultante è inferiore. Come è possibile questo? La risposta è la distanza. Più ci si allontana dalla Terra, minore è la forza gravitazionale, e il centro di E2 è a 6371 chilometri dalla superficie della Terra.
Ci sono abbastanza formiche per trasportare ogni umano.
Va bene, torniamo alla nostra domanda originale. Abbiamo ancora bisogno di sapere quanta forza di sollevamento può fornire una formica. Sto trovando numeri molto diversi su quanto una formica può sollevare, ma ho intenzione di usare il numero di 50 volte il loro peso corporeo. Combinate questo con un peso di formica di, diciamo, 2 milligrammi. 50 volte la loro massa sarebbe 100 milligrammi, risultando in una forza di sollevamento di 0,000981 Newton. Abbiamo bisogno di 1,4662378 * 10²⁵ Newton, quindi abbiamo bisogno di circa 1,49 * 10²⁸ formiche! Ora, la quantità totale di formiche su questo pianeta è stata stimata in 10¹⁶, quindi non abbiamo abbastanza formiche per sollevare il nostro pianeta. È interessante notare che, dato il nostro numero, ne abbiamo abbastanza per trasportare tutti gli esseri umani. 10¹⁶ formiche e 7,73 * 10⁹ umani, abbiamo più di un milione di formiche per ogni umano. Un milione di formiche di 2 milligrammi ciascuna hanno una massa totale di 2 kg. Potendo trasportare 50 volte la loro massa corporea, ne risultano 100 chilogrammi. L’uomo medio è molto più leggero di questo!