Gemiddelde snelheidsformule wordt gebruikt om de uniforme snelheid te vinden waarbij iets in een vast en gestaag tempo reist.
Voorbeeld, Een auto reist 3 uur. In het eerste uur legt hij 30 mijl af, in het tweede 45 mijl en in het derde 75 mijl.
Snelheid in het eerste uur = 30 mijl/uur
Snelheid in het tweede uur = 45 mijl/uur
Snelheid in het derde uur = 75 mijl/uur
We hebben drie verschillende snelheden in de drie uur durende reis.
Als we de gemiddelde snelheid voor de hele reis van drie uur willen vinden, moeten we de verhouding vinden tussen de totale afgelegde afstand en de totale tijdsduur.
Dat is, constante snelheid = (30 + 45 + 75) / 3
= 150 / 3
= 50 mijl / uur
Gebaseerd op het bovenstaande voorbeeld, de formule is om de gemiddelde snelheid te vinden is hieronder gegeven.
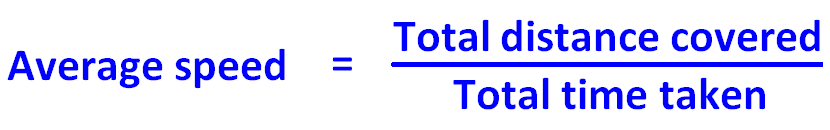
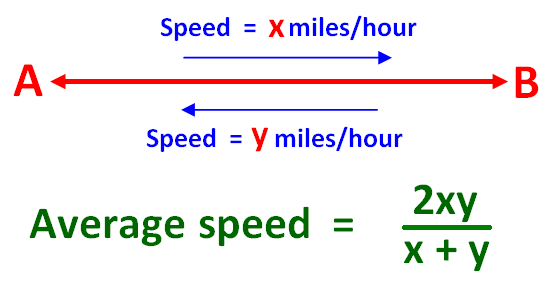
Als een persoon van A naar B reist met een bepaalde snelheid, zeg “x” mijl per uur. Hij komt terug van B naar A met een andere snelheid, zeg “y” mijl per uur. In beide gevallen legt hij dezelfde afstand af, maar met verschillende snelheden.
Dan is de formule om de gemiddelde snelheid voor de hele reis te vinden hieronder gegeven.
Gemiddelde snelheidsformule – Voorbeelden
Voorbeeld 1 :
David reed 3 uur met een snelheid van 50 mijl per uur, 2 uur met een snelheid van 60 mijl per uur en 5 uur met een snelheid van 70 mijl per uur. Wat was zijn gemiddelde snelheid gedurende de hele reis ?
Antwoord :
Stap 1 :
De formule voor de gemiddelde snelheid is
= Totale afstand / Totale tijd die is afgelegd.
En ook de formule voor de afstand is
= Snelheid ⋅ Tijd
Stap 2 :
Afgelegde afstand in de eerste 3 uur is
= 50 ⋅ 3
= 150 mijl
De in de volgende 2 uur afgelegde afstand is
= 60 ⋅ 2
= 120 mijl
Afgelegde afstand in de laatste 5 uur is
= 70 ⋅ 5
= 350 mijl
Stap 3 :
Dan, totale afstand is
= 150 + 120 + 350
= 620 mijl
Totale tijd is
= 3 + 2 + 5
= 10 uur
Step 4 :
Dus de gemiddelde snelheid is
= 620 / 10
= 62
Dus de gemiddelde snelheid voor de hele reis is 62 mijl per uur.
Voorbeeld 2 :
Jose reist van plaats A naar plaats B met een bepaalde snelheid. Als hij terugkomt van plaats B naar plaats A, is zijn snelheid 60 mijl per uur.Als de gemiddelde snelheid voor de hele reis 72 mijl per uur is, bereken dan zijn snelheid als hij van plaats A naar B reist.
Antwoord :
Step 1 :
Laat “a” de snelheid zijn van plaats A naar B.
Snelheid van plaats B naar A = 60 mijl/uur
Step 2 :
Hier legt hij in beide richtingen dezelfde afstand af.
Dan is de formule om de gemiddelde snelheid te vinden
= 2xy / (x + y)
Stap 3 :
x —-> Snelheid van plaats A naar B
x = a
y -.— Snelheid van plaats B naar A
y = 60
Step 4 :
Gegeven: de gemiddelde snelheid is 72 mijl/uur.
(2 ⋅ a ⋅ 60) / (a + 60) = 72
120a = 72(a + 60)
120a = 72a + 4320
48a = 4320
a = 90
Dus, de snelheid van plaats A naar B is 90 mijl per uur.
Voorbeeld 3 :
David reist van plaats A naar plaats B met een bepaalde snelheid. Als hij terugkomt van plaats B naar plaats A, verhoogt hij zijn snelheid 2 keer. Als de constante snelheid voor de hele reis 80 mijl per uur is, bepaal dan zijn snelheid als hij van plaats A naar B reist.
Antwoord :
Step 1 :
Laat “a” de snelheid zijn van plaats A naar B.
Dan is de snelheid van plaats B naar A = 2a
Step 2 :
De afgelegde afstand in beide richtingen (A naar B en B naar A) is gelijk.
Dus, de formule om de gemiddelde snelheid te vinden is
= 2xy / (x + y)
Stap 3 :
x —-> Snelheid van plaats A naar B
x = a
y -.— Snelheid van plaats B naar A
y = 2a
Step 4 :
Gegeven : Gemiddelde snelheid = 80 mijl/uur
(2 ⋅ a ⋅ 2a) / (a + 2a) = 80
4a² / 3a = 80
4a / 3 = 80
a = 60
Dus, de snelheid van plaats A naar B is 60 mijl per uur.
Voorbeeld 4 :
Een persoon doet er 5 uur over om van plaats A naar plaats B te reizen met een snelheid van 40 mijl per uur. Hij komt terug van plaats B naar plaats A met 25% toegenomen snelheid. Bereken de gemiddelde snelheid over de hele reis.
Antwoord :
Stap 1 :
Snelheid ( van A naar B ) = 40 mijl/uur
Snelheid ( van B naar A ) = 50 mijl/uur (25% toegenomen)
Step 2 :
De afgelegde afstand in beide richtingen (A naar B en B naar A) is gelijk.
Dus, de formule om de gemiddelde afstand te vinden is
= 2xy / (x + y)
Stap 3 :
x —-> Snelheid van plaats A naar B
x = 40
y -.— Snelheid van plaats B naar A
y = 50
Step 4 :
Gemiddelde snelheid = (2 ⋅ 40 ⋅ 50) / (40 + 50)
Gemiddelde snelheid = 44.44
Dus de gemiddelde snelheid voor de hele reis is ongeveer 44,44 mijl/uur.
Voorbeeld 5 :
Snelheid ( A naar B ) = 20 mijl/uur,
Snelheid (B naar C ) = 15 mijl/uur,
Snelheid (C naar D ) = 30 mijl/uur
Als de afstanden van A naar B, B naar C en C naar D gelijk zijn en het duurt 3 uur om van A naar B te reizen, bereken dan de gemiddelde snelheid van A naar D.
Antwoord :
Stap 1 :
Formule om afstand te vinden is
= Snelheid ⋅ Tijd
Afstand van A naar B is
= 20 ⋅ 3
= 60 mijl
Gegeven : De afstanden van A naar B, B naar C en C naar D zijn gelijk.
Totale afstand van A naar D is
= 60 + 60 + 60
= 180 mijl
Step 2 :
Formule om tijd te vinden is
= Afstand / Snelheid
Tijd (A naar B) = 60 / 20 = 3 uur
Tijd (B naar C) = 60 / 15 = 4 uur
Tijd (C naar D) = 60 / 30 = 2 uur
Totale tijd die nodig is van A tot D is
= 3 + 4 + 2
= 9 uur
Stap 3 :
Formule om gemiddelde snelheid te vinden is
= Totale afstand / Totale tijd
= 180 / 9
= 20
Dus, de gemiddelde snelheid van A naar D is 20 mijl per uur.

Om meer problemen te krijgen over de gemiddelde snelheid,
Klik hier
Naast de hierboven gegeven dingen, als u andere dingen nodig hebt, gebruik dan onze google aangepaste zoekopdracht hier.
Als u feedback over onze wiskunde-inhoud hebt, mail ons dan :
Wij stellen uw feedback altijd op prijs.
U kunt ook de volgende webpagina’s bezoeken over verschillende dingen in wiskunde.
WOORDPROBLEMEN
HCF en LCM woordproblemen
Woordproblemen over eenvoudige vergelijkingen
Woordproblemen over lineaire vergelijkingen
Woordproblemen over kwadratische vergelijkingen
Algebra-woordproblemen
Woordproblemen over treinen
Area en omtrek-woordproblemen
Woordproblemen over directe variatie en inverse variatie
Woordproblemen over eenheidsprijs
Woordproblemen bij eenheidstarief
Woordproblemen bij vergelijking van tarieven
Woordproblemen bij omrekening van gebruikelijke eenheden
Woordproblemen bij omrekening van metrieke eenheden
Woordproblemen bij enkelvoudige rente
Woordproblemen bij samengestelde rente
Woordproblemen bij soorten hoeken
Complementaire en supplementaire hoeken woordproblemen
Verdraaide feiten woordproblemen
Trigonometrie-woordproblemen
Percentage-woordproblemen
Winst en verlies-woordproblemen
Markeer- en aftekenwoordproblemen
Decimale-woordproblemen
Woordproblemen over breuken
Woordproblemen over gemengde breuken
Woordproblemen over éénstapsvergelijkingen
Woordproblemen over lineaire ongelijkheden
Ratio en proportie woordproblemen
Woordproblemen over sets en venndiagrammen
Woordproblemen over leeftijden
Woordproblemen over de stelling van Pythagoras
Percentage van een getal
Woordproblemen over constante snelheid
Woordproblemen over gemiddelde snelheid
Woordproblemen bij som van de hoeken van een driehoek is 180 graden
ANDERE TOPICS
Profit and loss shortcuts
Percentage shortcuts
Tijdentabel shortcuts
Tijd, snelheid en afstand
Ratio en proportie snelkoppelingen
Domein en bereik van rationale functies
Domein en bereik van rationale functies met gaten
Grafiek van rationale functies
Grafische rationale functies met gaten
Herhalende decimalen omzetten in breuken
Decimale representatie van rationale getallen
Kwadratische wortel vinden met behulp van lange deling
L.C.M methode voor het oplossen van tijd- en werkproblemen
Het omzetten van de woordproblemen in algebraïsche uitdrukkingen
Herkomst bij deling van 2 macht 256 door 17
Herkomst bij deling van 17 macht 23 door gedeeld door 16
Som van alle getallen van drie cijfers deelbaar door 6
Som van alle getallen van drie cijfers deelbaar door 7
Som van alle getallen van drie cijfers deelbaar door 8
Som van alle getallen van drie cijfers gevormd door 1, 3, 4
Som van alle drie getallen van vier cijfers gevormd met cijfers zonder nul
Som van alle drie getallen van vier cijfers gevormd met 0, 1, 2, 3
Som van alle drie getallen van vier cijfers gevormd met 1, 2, 5, 6