Die Formel für die Durchschnittsgeschwindigkeit wird verwendet, um die gleichmäßige Rate zu finden, bei der etwas in einem festen und gleichmäßigen Tempo fährt.
Beispiel: Ein Auto fährt 3 Stunden. In der ersten Stunde legt es 30 Meilen zurück, in der zweiten Stunde 45 Meilen und in der dritten Stunde 75 Meilen.
Geschwindigkeit in der ersten Stunde = 30 Meilen / Stunde
Geschwindigkeit in der zweiten Stunde = 45 Meilen / Stunde
Geschwindigkeit in der dritten Stunde = 75 Meilen / Stunde
Wir haben drei verschiedene Geschwindigkeiten in der dreistündigen Fahrt.
Wenn wir die Durchschnittsgeschwindigkeit für die gesamte dreistündige Fahrt finden wollen, müssen wir das Verhältnis zwischen der insgesamt zurückgelegten Strecke und der insgesamt benötigten Zeit finden.
Das ist, konstante Geschwindigkeit = (30 + 45 + 75) / 3
= 150 / 3
= 50 Meilen / Stunde
Ausgehend von dem obigen Beispiel, ist die Formel, um die Durchschnittsgeschwindigkeit zu finden, unten angegeben.
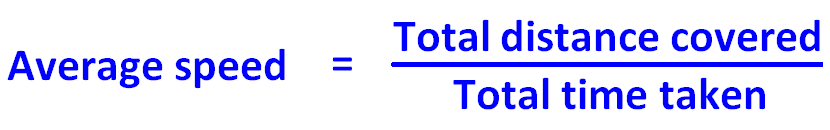
Wenn eine Person mit einer bestimmten Geschwindigkeit, sagen wir „x“ Meilen pro Stunde, von A nach B reist. Er kommt von B nach A mit einer anderen Geschwindigkeit zurück, sagen wir „y“ Meilen pro Stunde. Auf beiden Wegen legt er die gleiche Strecke zurück, aber mit unterschiedlichen Geschwindigkeiten.
Dann lautet die Formel, um die Durchschnittsgeschwindigkeit für die gesamte Strecke zu finden, wie folgt.
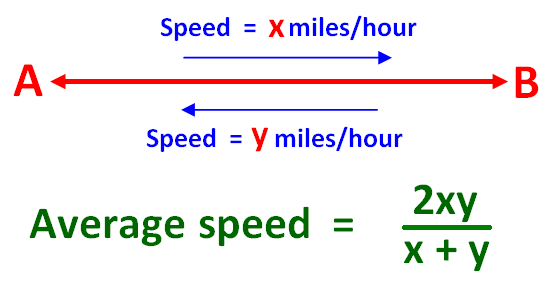
Durchschnittsgeschwindigkeit Formel – Beispiele
Beispiel 1 :
David fuhr 3 Stunden lang mit einer Geschwindigkeit von 50 Meilen pro Stunde, 2 Stunden lang mit 60 Meilen pro Stunde und 5 Stunden lang mit einer Geschwindigkeit von 70 Meilen pro Stunde. Wie hoch war seine Durchschnittsgeschwindigkeit während der gesamten Fahrt?
Antwort :
Schritt 1 :
Die Formel für die Durchschnittsgeschwindigkeit lautet
= Gesamtstrecke / Gesamtzeit.
Und auch die Formel für die Strecke lautet
= Geschwindigkeit ⋅ Zeit
Schritt 2 :
Die in den ersten 3 Stunden zurückgelegte Strecke beträgt
= 50 ⋅ 3
= 150 Meilen
Die in den nächsten 2 Stunden zurückgelegte Strecke beträgt
= 60 ⋅ 2
= 120 Meilen
Die zurückgelegte Entfernung in den letzten 5 Stunden ist
= 70 ⋅ 5
= 350 Meilen
Schritt 3 :
Dann, Gesamtstrecke ist
= 150 + 120 + 350
= 620 Meilen
Gesamtzeit ist
= 3 + 2 + 5
= 10 Stunden
Schritt 4 :
Die Durchschnittsgeschwindigkeit ist also
= 620 / 10
= 62
Die Durchschnittsgeschwindigkeit für die gesamte Reise ist also 62 Meilen pro Stunde.
Beispiel 2 :
Jose reist mit einer bestimmten Geschwindigkeit vom Ort A zum Ort B. Wenn er von Ort B nach Ort A zurückkommt, beträgt seine Geschwindigkeit 60 Meilen pro Stunde.
Wenn die Durchschnittsgeschwindigkeit für die gesamte Reise 72 Meilen pro Stunde beträgt, finde seine Geschwindigkeit, wenn er von Ort A nach B reist.
Antwort :
Schritt 1 :
Lassen Sie „a“ die Geschwindigkeit von Ort A nach B sein.
Geschwindigkeit von Ort B nach A = 60 Meilen/Stunde
Schritt 2 :
Hier legt er auf beiden Wegen die gleiche Strecke zurück.
Dann lautet die Formel zur Ermittlung der Durchschnittsgeschwindigkeit
= 2xy / (x + y)
Schritt 3 :
x —-> Geschwindigkeit von Ort A nach B
x = a
y —-> Geschwindigkeit von Ort B nach A
y = 60
Schritt 4 :
Gegeben: Die Durchschnittsgeschwindigkeit ist 72 Meilen/Stunde.
(2 ⋅ a ⋅ 60) / (a + 60) = 72
120a = 72(a + 60)
120a = 72a + 4320
48a = 4320
a = 90
So, beträgt die Geschwindigkeit von Ort A nach B 90 Meilen pro Stunde.
Beispiel 3 :
David reist mit einer bestimmten Geschwindigkeit vom Ort A zum Ort B. Wenn er von Ort B nach Ort A zurückkommt, erhöht er seine Geschwindigkeit um das 2-fache. Wenn die konstante Geschwindigkeit für die gesamte Reise 80 Meilen pro Stunde beträgt, finden Sie seine Geschwindigkeit, wenn er von Ort A nach B reist.
Antwort :
Schritt 1 :
Lassen Sie „a“ die Geschwindigkeit von Ort A nach B sein.
Dann sei die Geschwindigkeit von Ort B nach A = 2a
Schritt 2 :
Die auf beiden Wegen (A nach B und B nach A) zurückgelegte Strecke ist gleich.
Die Formel zur Ermittlung der Durchschnittsgeschwindigkeit lautet also
= 2xy / (x + y)
Schritt 3 :
x —-> Geschwindigkeit von Ort A nach B
x = a
y —-> Geschwindigkeit von Ort B nach A
y = 2a
Schritt 4 :
Gegeben: Durchschnittsgeschwindigkeit = 80 Meilen/Stunde
(2 ⋅ a ⋅ 2a) / (a + 2a) = 80
4a² / 3a = 80
4a / 3 = 80
a = 60
So, die Geschwindigkeit von Ort A nach B beträgt 60 Meilen pro Stunde.
Beispiel 4 :
Eine Person braucht 5 Stunden, um von Ort A nach Ort B mit einer Geschwindigkeit von 40 Meilen pro Stunde zu fahren. Er kommt von Ort B nach Ort A mit 25% erhöhter Geschwindigkeit zurück. Ermitteln Sie die Durchschnittsgeschwindigkeit für die gesamte Reise.
Antwort :
Schritt 1 :
Geschwindigkeit ( von A nach B ) = 40 Meilen/Stunde
Geschwindigkeit ( von B nach A ) = 50 Meilen/Stunde (25% erhöht)
Schritt 2 :
Die zurückgelegte Strecke ist auf beiden Wegen (A nach B und B nach A) gleich.
Die Formel zur Ermittlung der durchschnittlichen Entfernung lautet also
= 2xy / (x + y)
Schritt 3 :
x —-> Geschwindigkeit von Ort A nach B
x = 40
y —-> Geschwindigkeit von Ort B nach A
y = 50
Schritt 4 :
Durchschnittsgeschwindigkeit = (2 ⋅ 40 ⋅ 50) / (40 + 50)
Durchschnittsgeschwindigkeit = 44.44
Die Durchschnittsgeschwindigkeit für die gesamte Strecke beträgt also etwa 44,44 Meilen/Stunde.
Beispiel 5 :
Geschwindigkeit (A nach B) = 20 Meilen/Stunde,
Geschwindigkeit (B nach C) = 15 Meilen/Stunde,
Geschwindigkeit (C bis D ) = 30 Meilen/Stunde
Wenn die Entfernungen von A nach B, B nach C und C nach D gleich sind und man für die Strecke von A nach B 3 Stunden braucht, finde die Durchschnittsgeschwindigkeit von A nach D.
Antwort :
Schritt 1 :
Formel zur Ermittlung der Entfernung ist
= Rate ⋅ Zeit
Die Entfernung von A nach B ist
= 20 ⋅ 3
= 60 Meilen
Gegeben: Die Entfernungen von A nach B, B nach C und C nach D sind gleich.
Gesamtentfernung von A nach D ist
= 60 + 60 + 60
= 180 Meilen
Schritt 2 :
Formel zur Ermittlung der Zeit lautet
= Entfernung / Geschwindigkeit
Zeit (A nach B) = 60 / 20 = 3 Stunden
Zeit (B nach C) = 60 / 15 = 4 Stunden
Zeit (C bis D) = 60 / 30 = 2 Stunden
Die Gesamtzeit von A bis D ist
= 3 + 4 + 2
= 9 Stunden
Schritt 3 :
Formel zur Ermittlung der Durchschnittsgeschwindigkeit lautet
= Gesamtstrecke / Gesamt Zeit
= 180 / 9
= 20
So, beträgt die Durchschnittsgeschwindigkeit von A nach D 20 Meilen pro Stunde.

Um mehr Probleme mit der Durchschnittsgeschwindigkeit zu bekommen,
Bitte klicken Sie hier
Abgesehen von den oben genannten Sachen, wenn Sie andere Sachen brauchen, benutzen Sie bitte unsere Google Custom Search hier.
Wenn Sie ein Feedback zu unseren Mathe-Inhalten haben, mailen Sie uns bitte:
Wir freuen uns immer über Ihr Feedback.
Sie können auch die folgenden Webseiten zu verschiedenen Themen der Mathematik besuchen.
WORTPROBLEME
HCF- und LCM-Wortaufgaben
Wortaufgaben zu einfachen Gleichungen
Wortaufgaben zu linearen Gleichungen
Wortaufgaben zu quadratischen Gleichungen
Algebra Wortprobleme
Wortprobleme zu Zügen
Flächen- und Umfangs-Wortprobleme
Wortprobleme zu direkter Variation und inverser Variation
Wortprobleme zu Einheitspreis
Wortaufgaben zum Einheitskurs
Wortaufgaben zum Vergleich von Kursen
Wortaufgaben zur Umrechnung von gebräuchlichen Einheiten
Wortaufgaben zur Umrechnung von metrischen Einheiten
Wortaufgaben zum einfachen Zinsen
Wortaufgaben zu Zinseszinsen
Wortaufgaben zu Winkelarten
Wortaufgaben zu Komplementär- und Ergänzungswinkeln
Wortaufgaben zu Doppelfakten
Trigonometrie-Wortaufgaben
Prozentsatz-Wortaufgaben
Gewinn- und Verlust-Wortaufgaben
Markierungs- und Markierungs-Wortaufgaben
Dezimal-Wortaufgaben
Wortaufgaben zu Brüchen
Wortprobleme zu gemischten Brüchen
Wortprobleme zu Einschrittgleichungen
Wortprobleme zu linearen Ungleichungen
Wortprobleme zu Verhältnissen und Proportionen
Wortprobleme zu Zeit und Arbeit
Wortprobleme zu Mengen und Venn-Diagrammen
Wortaufgaben zu Altersangaben
Wortaufgaben zum Satz des Pythagoras
Prozent einer Zahl Wortaufgaben
Wortaufgaben zur konstanten Geschwindigkeit
Wortaufgaben zur Durchschnittsgeschwindigkeit
Wortaufgaben zu Summe der Winkel eines Dreiecks ist 180 Grad
SONSTIGE THEMEN
Gewinn- und Verlustkürzel
Prozentkürzel
Zeittabellekürzel
Zeit, Geschwindigkeits- und Entfernungsabkürzungen
Verhältnis- und Proportionsabkürzungen
Bereich und Bereich rationaler Funktionen
Bereich und Bereich rationaler Funktionen mit Löchern
Grafische Darstellung rationaler Funktionen
Grafische Darstellung rationaler Funktionen mit Löchern
Umwandeln von sich wiederholenden Dezimalzahlen in Brüche
Dezimaldarstellung rationaler Zahlen
Finden der Quadratwurzel durch lange Division
L.C.M-Methode zum Lösen von Zeit- und Arbeitsaufgaben
Umwandlung der Wortaufgaben in algebraische Ausdrücke
Rest, wenn 2 hoch 256 durch 17 geteilt wird
Rest, wenn 17 hoch 23 durch 16 geteilt wird
Summe aller dreistelligen Zahlen, die durch 6 teilbar sind
Summe aller dreistelligen Zahlen, die durch 7 teilbar sind
Summe aller dreistelligen Zahlen, die durch 1, 3, 4 gebildet werden
Summe aller dreistelligen Zahlen, die durch 1, 3, 4
Summe aller drei vierstelligen Zahlen, die mit Nicht-Null-Ziffern gebildet werden
Summe aller drei vierstelligen Zahlen, die mit 0, 1, 2, 3 gebildet werden
Summe aller drei vierstelligen Zahlen, die mit 1, 2, 5, 6 gebildet werden