Guinguette Marais Poitevin

Metoda 3-4-5 dla wyrównania narożników

Przez Roberta Robillarda na Home Repairs And Remodeling

Metoda 3-4-5 Trójkątów

Cieślarstwo nie jest nauką ścisłą; jest to pragmatyczne podejście do rozwiązywania problemów, budowania i naprawiania. Moje doświadczenie nauczyło mnie, że kilka podstawowych zasad prowadzi nas do tego, co będzie lub nie będzie działać. Pion, Poziom i Kwadrat to niektóre z tych zasad.

3-4-5 Reguła Zapewniająca Kwadratowe Układy

Stolarze i budowniczowie często używają metody 3-4-5 do wyrównywania narożników i zapewniają, że projekty, które budują mają dokładny kąt 90 stopni.

W świecie mieszkalnym i budowlanym stolarze często używają kwadratów prędkości i kwadratów ramowych do sprawdzania układów.

Gdy układ jest duży, te kwadraty ramowe są po prostu zbyt małe, aby zagwarantować potrzebną dokładność. Duże przebudowy i projekty budowlane, takie jak układanie fundamentów domu lub ścian często wykorzystują technikę trójkątów 3-4-5, aby zapewnić dokładne kąty 90 stopni.

Unikaj błędów potęgujących

Niezależnie od tego, nad jakim projektem pracujesz, jeśli twoja podstawa lub fundament nie jest równa, pionowa i kwadratowa, reszta projektu będzie nie do zrobienia. Błędy na podstawie pokładu, domu lub ganku będzie nadal rosnąć i składać się do czasu dostać się do wykończenia wykończenia, szafki, lub dotrzeć do dachu ramki.

3-4-5 Reguła Layman’s Terms:

Jeśli krótszy bok trójkąta ma 3 stopy, a noga, która rozciąga się od niego pod kątem 90 stopni ma 4 stopy, to przeciwprostokątna, czyli najdłuższa noga, będzie miała 5 stóp.

Ta technika wymaga po prostu, aby stolarz stworzył trójkąt w rogu linii, które mają być kwadratowe (90 stopni) względem siebie.

Trójkąt 3-4-5 musi mieć

• Jeden bok (noga trójkąta) o długości 3 stóp
• Drugi bok (noga trójkąta) o długości 4 stóp
• Trzeci bok, łączący dwie nogi o długości 5 stóp

Każdy trójkąt o bokach 3, 4 i 5 stóp będzie miał kąt 90 stopni naprzeciwko boku o długości 5 stóp. Piękno i prostota tej techniki polega na tym, że jeśli stolarz lub budowniczy potrzebuje zwiększyć dokładność na większych ścianach lub konstrukcjach, można zastosować dowolną wielokrotność reguły 3-4-5.

Przykłady Reguły 3-4-5

• 3-4-5
• 6-8-10
• 9-12-15
• 12- 16-20
• 15-20-25

Dlaczego to działa?

Matematycznie rzecz biorąc, dlaczego metoda 3-4-5 przy dzieleniu kątów tworzy idealny kąt prosty?

W geometrii, dobrze znaną metodą konstruowania kąta prostego jest zastosowanie Twierdzenia Pitagorejskiego. Matematyk, Pitagoras, odkrył związek pomiędzy bokami trójkąta prostokątnego, który jest obecnie znany jako Twierdzenie Pitagorejskie. Pitagoras udowodnił, że kwadrat najdłuższego boku (hipotensji) jest równy sumie kwadratów pozostałych dwóch boków.

Zapisuje się to w postaci następującego równania:

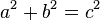
A i B to dwie nogi trójkąta prostego, a C to hipotensja. Jeśli podstawimy liczby z trójkąta 3-4-5 do tego wzoru, będziemy mieli 9″ + 16″ = 25″

Pamiętanie 3-4-5

Używanie wymiarów trójkątów 3, 4 i 5 jest łatwe do zapamiętania i zastosowania. Nie ma trudnych równań do zapamiętania, a metoda 3-4-5 zawsze stworzy doskonały kąt prosty za każdym razem.