To pytanie jest bardziej skomplikowane, niż mogłoby się wydawać

Ile mrówek potrzeba, aby unieść Ziemię? To pytanie może wydawać się bardzo proste. Zasadniczo, musielibyśmy wiedzieć dwie rzeczy: 1, jak dużą masę może unieść jedna mrówka, oraz 2, jaką masę ma Ziemia. Podziel drugą liczbę przez pierwszą, a otrzymasz pożądaną odpowiedź. Prawda?
Po pierwsze, musimy zdecydować, gdzie zamierzamy podnieść Ziemię w naszym małym eksperymencie myślowym. Zazwyczaj, gdy zadajemy pytania typu „Ile X potrzeba, aby podnieść Y”, mamy na myśli „na Ziemi”. W tym celu musimy podnieść Ziemię na Ziemi, ale ponieważ jest to eksperyment myślowy, nie pozwólmy, aby to przeszkodziło. Załóżmy, że jesteśmy na Ziemi i mamy „drugą Ziemię”, E2, którą chcemy, aby nasze mrówki podniosły. Wszystko, co jest ważne o E2 to to, że ma taką samą masę, formę i rozmiar jak nasza Ziemia.
E2 ma pole grawitacyjne równe polu grawitacyjnemu Ziemi.
Okay, więc teraz możemy po prostu podzielić masę E2 przez to, ile masy jedna mrówka może podnieść, tak jak powiedzieliśmy, prawda? Nie do końca. Pytanie jest nieco bardziej skomplikowane niż to. Widzisz, ta metoda działa dla „normalnych” obiektów, takich jak książka, kamień, czy nawet autobus. E2 jest jednak od nich znacznie cięższy. Tak bardzo, że posiada pole grawitacyjne równe polu grawitacyjnemu Ziemi (ponieważ jego masa jest równa masie Ziemi). W przypadku normalnych spadających obiektów musimy brać pod uwagę tylko pole grawitacyjne Ziemi, a nie pole grawitacyjne obiektu, które w rzeczywistości nie istnieje. W takiej sytuacji możemy łatwo obliczyć siłę, z jaką Ziemia oddziałuje na obiekt, mnożąc masę obiektu w kilogramach przez 9,81, aby otrzymać siłę w niutonach. E2 jest jednak na to za ciężki.
To, co musimy wiedzieć, to siła utrzymująca naszego hipotetycznego E2 względem Ziemi.
To, co musimy wiedzieć, to siła utrzymująca naszego hipotetycznego E2 względem Ziemi. Następnie możemy obliczyć, ile mrówek potrzeba, aby przeciwdziałać tej sile. Siłę utrzymującą E2 na dole można obliczyć za pomocą następującego wzoru, obliczając siłę F między dwiema masami (obie oznaczane symbolem m) o odległości r między nimi:
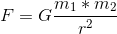
G jest stałą grawitacyjną. Jeśli E2 „siedzi” na Ziemi, to środki obu mas są oddalone od siebie o 12742000 metrów (dwukrotność promienia Ziemi). Wypełnienie reszty liczb we wzorze daje nam siłę 1,4662378 * 10²⁵ Newtona. Co ciekawe, liczba ta jest kilka razy MNIEJSZA niż byłaby, gdybyśmy (błędnie) obliczali siłę tak, jak to robimy dla „normalnych” obiektów spadających na Ziemię (mnożąc przez 9,81). Mimo, że mamy w grze dodatkowe ciało grawitacyjne z własną siłą, to wypadkowa siła jest mniejsza. Jak to jest możliwe? Odpowiedzią jest odległość. Im dalej od Ziemi, tym siła grawitacji jest mniejsza, a środek E2 jest oddalony od powierzchni Ziemi o 6371 kilometrów.
Jest wystarczająco dużo mrówek, by unieść każdego człowieka.
W porządku, wracamy do naszego pierwotnego pytania. Nadal musimy wiedzieć, jak dużą siłę nośną może zapewnić mrówka. I’m finding wildy different numbers on how much an ant can lift, but I’m going to use the number of 50 times their own body weight. Połącz to z wagą mrówki, powiedzmy, 2 miligramy. 50-krotność ich masy to 100 miligramów, co daje siłę nośną równą 0,000981 niutona. Potrzebujemy 1,4662378 * 10²⁵ Newtona, więc potrzebujemy około 1,49 * 10²⁸ mrówek! Całkowita liczba mrówek na naszej planecie została oszacowana na 10¹⁶, więc nie mamy prawie tyle mrówek, aby unieść naszą planetę. Co ciekawe, biorąc pod uwagę nasze liczby, mamy ich wystarczająco dużo, aby unieść wszystkich ludzi. 10¹⁶ mrówek i 7,73 * 10⁹ ludzi, mamy ponad milion mrówek na każdego człowieka. Milion mrówek o masie 2 miligramów każda ma łączną masę 2 kg. Będąc w stanie unieść 50-krotność swojej masy ciała, daje to 100 kilogramów. Przeciętny człowiek jest od tego znacznie lżejszy!